Meta
˅ Inhaltsverzeichnis
Zwei-Seiten-Form
Das fundamentale Prinzip der soziologischen Systemtheorie besteht darin, dass sie nicht von Einheit, sondern Differenz ausgeht. Dies kommt zuvorderst in der für die Theorie konstitutiven Unterscheidung von System als Einheit der Differenz von System und Umwelt zum Ausdruck. Ursprünglich vom differenztheoretischen Ansatz in den sprachwissenschaftlichen Vorlesungen von Ferdinand de Saussure inspiriert, hat Niklas Luhmann in den 1990er-Jahren den differenztheoretischen Ansatz von George Spencer-Brown übernommen und in seine Theorie eingearbeitet. Wie er in seiner «Einführung in die Systemtheorie» bemerkt, soll es sich dabei um «die radikalste Form eines solch differenzialistischen Denkens» handeln (2020: 68).
In seinem Buch «Laws of Form» (LoF) entwickelt Spencer-Brown ein Indikationenkalkül mit dem Anspruch, Mathematik mit einer primären Arithmetik und primären Algebra auf eine gemeinsame Basis abzustellen und unter Verwendung imaginärer Werte mit Gleichungen zweiten Grades zu erweitern. Als Ausgangspunkt seiner Überlegungen wählt er die Operation des Unterscheidens.
Bei der Entwicklung seines Indikationenkalküls schwächt Spencer-Brown die klassischen mathematischen Prämissen derart ab, dass es über die blosse Mathematik hinausreicht. «Spencer-Brown», so Athanasios Karafillidis in seinem Buch «Soziale Formen», «rekonstruiert […] Strukturen, die allen mathematischen, linguistischen, physikalischen und biologischen (und man darf hinzufügen: philosophischen und soziologischen) Formen zugrunde liegen» (2010: 117). Damit hat er ein Kalkül geschaffen, dessen Anziehungs- und Strahlkraft weit über die Mathematik hinausreicht.
Für sein Indikationenkalkül hat Spencer-Brown eine eigene formale Sprache und ein Notationssystem geschaffen, das im Kontext der Systemtheorie von Luhmann übernommen und später insbesondere von Dirk Baecker weiter ausgearbeitet worden ist. Im Folgenden werden wir die Sprache und Notation von Spencer-Brown in den Unterabschnitten Schritt für Schritt durchgehen und in den eingerahmten Textabschnitten durch systemtheoretische Interpretationen ergänzen.

Spencer-Brown führt seinen Indikationenkalkül in den «Laws of Form» nicht mit einer deduktiven Methode ein, sondern entwickelt ihn in einem iterativen Konstruktionsprozess. Dieser beginnt mit der viel zitierten Anweisung: «Draw a distinction» – Treffe eine Unterscheidung. Durch den Vollzug dieser Anweisung entsteht die Unterscheidung der Form.
˅ Unterscheiden
Zu Beginn des zweiten Kapitels der LoF formuliert Spencer-Brown die Anweisung: «Draw a distinction» (2015: 3). Durch den Vollzug dieser Anweisung entsteht die Unterscheidung der Form. Sie zeichnet sich durch vier Aspekte aus: die Grenze, die Seite links und die Seite rechts der Grenze sowie den Kontext der Unterscheidung.
Zentral für das Verständnis dieser vier Aspekte ist Spencer-Browns Definition des Begriffs der Unterscheidung im ersten Kapitel der LoF: «Distinction is perfect continence» (2015: 1). Diese Definition wird in der Sekundärliteratur als «Unterscheidung ist vollkommener Zusammenhang» (vgl. Varga von Kibéd/Matzka 2016: 58) oder «Trennung ist (sein Gegenteil) Verbindung» (vgl. Schönwälder-Kuntze/Wille 2009: 71) interpretiert.
Diese widersprüchlich anmutende Definition ist gleich in zwei Hinsichten von Bedeutung: Einerseits trennt die Unterscheidung der Form zwei Seiten und weist gleichzeitig auf deren untrennbaren Zusammenhang hin. Andererseits grenzt sich die Form der Unterscheidung von anderen Formen der Unterscheidung ab und verweist damit auf einen kontextuellen Zusammenhang.
Offensichtlich haben wir es beim Kalkül mit zwei Unterscheidungen zu tun, nämlich mit der operativen Unterscheidung der Form (vertikaler Strich) und mit der beobachtbaren Form der Unterscheidung.
^ ^ ^
Die Form
Bezeichnenderweise geht Niklas Luhmann im Kapitel «Die Unterscheidung von System und Umwelt» in «Die Gesellschaft der Gesellschaft» näher auf die Zwei-Seiten-Form ein. «Formen», so Luhmann, «sind […] nicht länger als (mehr oder weniger schöne) Gestalten zu sehen, sondern als Grenzlinien, als Markierungen einer Differenz, die dazu zwingt, klarzustellen, welche Seite man bezeichnet, das heisst: auf welcher Seite der Form man sich befindet und wo man dementsprechend für weitere Operationen anzusetzen hat. Die andere Seite der Grenzlinie (der ‹Form›) ist gleichzeitig mitgegeben» (1997: 60).
Einheit der Form
Die Einheit der Form ist nach Luhmann das «ausgeschlossene Dritte, das nicht beobachtet werden kann, solange man mit der Form beobachtet» (vgl. 1997: 62). Im Unterschied zur operativen Unterscheidung der Form haben wir die Einheit der Form als Form der Unterscheidung bezeichnet. Wie unter dem Titel «Operation und Beobachtung» diskutiert, kann ein Beobachter nicht in einem Zug eine Unterscheidung (Unterscheidung der Form) treffen und dabei noch die verwendete Unterscheidung (Form der Unterscheidung) beobachten. Dazu bräuchte es einer Beobachtung zweiter Ordnung.
Nach Spencer-Brown kann keine Unterscheidung getroffen werden, ohne auf die eine oder andere Seite der Unterscheidung hinzuweisen.
˅ Hinweisen
Nach Spencer-Brown besteht ein enger Zusammenhang zwischen Unterscheiden und Hinweisen. Das erste Kapitel der LoF beginnt mit dem Satz: «We take as given the idea of distinction and the idea of indication, and that we cannot make an indication without drawing a distinction» (2015: 1).
Das Hinweisen wird durch einen am vertikalen Strich (Grenze) abzweigenden waagrechten Strich (Hinweis) angezeigt. Dadurch entsteht ein Haken, der die Unterscheidung der Form in eine markierte Innenseite (m) und eine unmarkierte Aussenseite (n) teilt. Jede Unterscheidung erhält so zwei Referenzpunkte (m, n). An dieser Stelle geht es nicht darum, was markiert, sondern dass markiert wird. Es handelt sich zunächst um keine inhaltliche, sondern um eine rein formale Unterscheidung.
Das dergestalt eingeführte Elementarzeichen des Indikationenkalküls, der Haken, hat eine deskriptive (beschreibende) und eine injunktive (auffordernde) Bedeutung. Einerseits markiert der Haken («mark») eine bereits getroffene Unterscheidung. Andererseits fordert der Haken («cross») dazu auf, die Unterscheidung selbst zu treffen.
Diese Doppeldeutigkeit macht deutlich, dass anders als in der klassischen Mathematik, in der zwischen Operanden (Zeichen für Zahlen) und Operator (Zeichen für Rechenoperationen) unterschieden wird, bei Spencer-Brown Operand und Operator in einem einzigen Elementarzeichen zusammenfallen.
^ ^ ^
Die operative Unterscheidung der Form wird erst durch den Kontext der Unterscheidung zu einer beobachtbaren Form der Unterscheidung transformiert.
˅ Kontextualisieren
Unterscheiden und Hinweisen vollziehen sich immer in einem Kontext. Spencer-Brown spricht in diesem Zusammenhang zunächst von Räumen, Zuständen oder Inhalten (vgl. 2015: 3). Entgegen unserer ersten Intuition fasst er nun nicht bloss die markierte Seite (m) einer Unterscheidung, sondern auch deren unmarkierte Seite (n) als Teil der Form auf: «Call the space cloven by any distinction, togehter with the entire content oft the space, the form of the distincion» (ebd.). Die Unterscheidung der Form transformiert sich also erst durch den Kontext zu einer Form der Unterscheidung.
Die Form der Unterscheidung wiederum markiert ebenfalls eine Grenze innerhalb des Möglichkeitsspielraums anderer Formen der Unterscheidungen. Deshalb kann ihre Aussenseite ebenfalls als unmarkiert (n) ausgezeichnet werden («unwritten cross»). «Die Beobachtung von Formen», so Karafillidis, «ist deshalb nicht abschliessbar und führt zu keinem natürlichen Ende, zu keiner abschliessenden Gewissheit. Unausweichlich wird die unmarkierte Aussenseite immerfort mitgeführt» (2015: 126).
Die Zwei-Seiten-Form markiert also immer drei Seiten: die markierte Innenseite (m) und die unmarkierte Aussenseite (n) der Unterscheidung der Form sowie die unmarkierte Aussenseite der Form der Unterscheidung (n).
^ ^ ^
Nur wenn die Inhalte der Unterscheidung eine Wertdifferenz aufweisen, dann besteht ein Motiv, die Unterscheidung zu treffen.
˅ Differenzieren
Nachdem Spencer-Brown die Unterscheidung der Form als vollkommenen Zusammenhang definiert hat, erklärt er: «There can be no distiction without motive, and there can be not motive unless contents are seen to differ in value» (2015: 1). Damit führt Spencer-Brown zwei weitere Aspekte des Indikationenkalküls ein, nämlich das Motiv und die Differenz.
Beginnen wir mit dem Motiv. War mit Blick auf den Kontext der Unterscheidung der Form bisher von Räumen, Zuständen oder Inhalten die Rede, fokussiert Spencer-Brown nun auf letztere («contents»). Denn nur wenn die Inhalte einer Unterscheidung als von verschiedenem Wert gesehen werden, besteht ein Motiv, eine Unterscheidung zu treffen. Dieses Motiv fiele weg, würden die Inhalte von gleichem Wert gesehen.
Es braucht also eine Differenz. Sie bildet die Bedingung der Möglichkeit, auf den Wert eines Inhalts hinzuweisen. Eine Wertdifferenz zu sehen, ist jedoch nur möglich, wenn die unterschiedenen Inhalte auch von Wert sind. Deshalb setzen wir die Variable a für den Wert des Inhalts auf der markierten Seite (m) und die Variable b für den Wert des Inhalts auf der unmarkierten Seite (n). Die Einheit einer Unterscheidung kann also auch als Einheit einer Differenz aufgefasst werden.
Differenz und Unterscheidung führen zu einer eigentümlichen Zirkularität: Einerseits ist die Differenz das Resultat einer Unterscheidung; andererseits ist sie Voraussetzung dafür, eine Unterscheidung zu treffen.
Matthias Varga von Kibéd und Rudolf Matzka halten diesbezüglich in ihrem Beitrag im Buch «Kalkül der Form» fest: «In dieser scheinbaren Zirkularität liegt zugleich eine Andeutung, wie Formentstehung mit Begriffsbildung verbunden ist […]: Wäre vor der Bildung eines Begriffs der durch ihn zu charakterisierende Unterschied schon vollständig gegeben, wäre seine Einführung überflüssig. Wäre allerdings kein Unterschied gegeben, wäre seine Einführung unmöglich. Eine Verschiedenheit [Differenz, Anm. CMS] kann man sich im Sinne der topologischen Metaphern Spencer Browns vielleicht am günstigsten durch eine nicht ganz undurchlässige Grenze vorstellen» (2016: 63).
Schliesslich führt Spencer-Brown noch den Aspekt des Namens ein: «If a content is of value, a name can be taken to indicate this value» (ebd.). Der Indikationenkalkül sieht zwei Möglichkeiten vor, einen Namen zu verwenden, um auf den Wert eines Inhalts hinzuweisen: mal mit der Nennung eines Namens («calling of the name»), mal durch die Absicht zur Überquerung der Grenze («crossing of the boundary»).
Hinsichtlich der ersten Möglichkeit gilt: Die Nennung des Namens kann mit dem Wert des Inhalts identifiziert werden. Das heisst an unserem Beispiel, mit der Nennung des Namens a kann auf die Variable a hingewiesen werden. Es ist leicht zu sehen, dass in diesem Fall die deskriptive Bedeutung des oben eingeführten Hakens als «mark» zum Tragen kommt. Eine solche Markierung bezeichnet einen Unterschied, macht ihn aber nicht.
Vor dem Hintergrund dieser Setzung formuliert Spencer-Brown das 1. Axiom («The Law of calling») des Indikationenkalküls: «The value of a call made again is the value of the call» (2015: 2). Das bedeutet, dass sich der Wert des Namens – und damit der Wert des Inhalts – bei wiederholter Nennung des Namens nicht ändert («to recall is to call»).
Bemerkenswert am 1. Axiom ist, dass bei der wiederholten Nennung des Namens der Informationsgehalt der Differenz und damit auch der Motivlage gleich bleibt. Spencer-Brown schafft damit die Grundlage für die sogenannte Gedächtnisfunktion formaler Systeme.
Hinsichtlich der zweiten Möglichkeit gilt: Mit der Überquerung der Grenze der Unterscheidung kann der Wert des Inhalts identifiziert werden. Das heisst an unserem Beispiel, mit dem Übergang von der unmarkierten Seite (n) zur markierten Seite (m) wird auf die Variable a hingewiesen. In diesem Fall kommt die injunktive Bedeutung des Hakens («cross») zum Tragen. Eine solche Aufforderung zur Überquerung macht einen Unterschied, ist im Moment des Unterscheidens aber nicht markierbar.
Vor dem Hintergrund dieser Setzung formuliert Spencer-Brown das 2. Axiom («The Law of crossing»): «The value of a crossing made again is not the value of the crossing» (ebd.). Das bedeutet, dass mit der ersten Überquerung der Grenze, von der unmarkierten zur markierten Seite, zwar der Wert der Überquerung – und damit der Wert eines Inhaltes – identifiziert wird. Das Axiom besagt nun, dass sich bei einer erneuten Überquerung, diesmal von der markierten zur unmarkierten Seite, der Wert der Überquerung – und damit der Wert des Inhaltes – verändert («recross is not to cross»).
Das erneute Überqueren der Grenze hat also zwei Folgen: Einerseits wird der mit der ersten Überquerung («cross») identifizierte Wert des Inhaltes aufgehoben bzw. entwertet; andererseits wird mit der erneuten Überquerung («recross») der Wert des Inhalts auf der anderen Seite identifiziert.
Bemerkenswert am 2. Axiom ist, wenn eine Absicht zur Überquerung und dann eine Absicht zur Rücküberquerung besteht, dann entspricht der Wert der beiden Absichten zusammengenommen weder dem Wert des Inhalts auf der einen noch auf der anderen Seite. Diese Eigenheit wird im Zusammenhang mit dem Wiedereinführen nochmals aufgegriffen.
^ ^ ^
Im Kapitel «Die Unterscheidung von System und Umwelt» in «Die Gesellschaft der Gesellschaft» nimmt Luhmann die zwei Axiome von Spencer-Brown wie folgt auf: «Kreuzen ist kreativ. Denn während die Wiederholung einer Bezeichnung nur deren Identität bestätigt […], ist das Hin- und Herkreuzen keine Wiederholung und kann daher auch nicht zu einer einzigen Identität zusammengezogen werden. Das ist nur eine andere Version für die Einsicht, dass eine Unterscheidung sich bei ihrem Gebrauch nicht selbst identifizieren kann» (1997: 61)
Mit der Wiedereinführung wird nach Spencer-Brown die Form der Unterscheidung in die Unterscheidung der Form wieder eingeführt, was zu einem imaginären Zustand führt.
˅ Wiedereinführen
In den letzten zwei Kapiteln der LoF führt Spencer-Brown die Wiedereinführung («re-entry») ein. Sie steht für eine Operation, die die Unterscheidung in das Unterschiedene wieder einführt. Im Notationssystem der LoF wird die Wiedereinführung mit einem umgekehrten Haken dargestellt, der die markierte Aussenseite der Form der Unterscheidung in die Innenseite der Unterscheidung der Form zurückführt.
Der «re-etnry» ist der meistdiskutierte Begriff der LoF. Dies hat nicht zuletzt damit zu tun, dass Struktur und Dynamik der so bezeichneten Operationen eine gewisse Ähnlichkeit mit anderen Begriffen haben. Dazu zählen etwa: «Resonanz», «Feedback», «Rückkopplung», «Reflexivität», «Selbstreferenz», «Rekursion», «Zirkularität» u.a. Katrin Wille erinnert daran, dass Spencer-Brown an manchen Stellen auf eine «Familienähnlichkeit» zwischen diesen Begriffen und dem «re-entry» hinweist (vgl. 2009: 191). In den LoF indes demonstriert er die Operation der Wiedereinführung anhand der Erweiterung seiner primären Arithmetik.
Im Kapitel über Gleichen zweiten Grades formt Spencer-Brown einen Ausgangsausdruck in fünf Schritten so um, dass der Ausgangsausdruck verdoppelt und nach weiteren fünf Schritten verdreifacht wird (vgl. 2015: 45f). Da sich die Konstruktionsanweisung mit den fünf Umformungsschritten beliebig wiederholen lässt, lässt sich auch der Ausgangsausdruck beliebig verlängern. Die dergestalt durchgeführte Wiedereinführung transformiert Gleichungen ersten in Gleichungen zweiten Grades.
Die Möglichkeit, einen Ausgangsausdruck beliebig zu verlängern, verletzt allerdings eine zentrale Regel der Algebra. Diese besagt, dass eine Gleichung nur aus endlichen Umformungsschritten bestehen darf, da ihr Wert ansonsten nicht bestimmt werden kann. Wie also lässt sich der Wert von Gleichungen zweiten Grades bestimmen?
Die Antwort liegt nach Spencer-Brown in der Möglichkeit, die verschiedenen Fälle der Wertbelegungen an den Gleichungen ersten und zweiten Grades durchzuspielen und miteinander zu vergleichen. Interpretieren wir eine Zwei-Seiten-Form ohne Wiedereinführung als Gleichung ersten Grades, dann sehen die verschiedenen Wertbelegungen wie folgt aus:
- Ist die Innenseite der Unterscheidung markiert (m) und die Aussenseite der Unterscheidung unmarkiert (n), dann ist der Wert der Gleichung markiert (m).
- Ist die Innen- und Aussenseite der Unterscheidung markiert (m), dann ist der Wert der Gleichung unmarkiert (n).
- Ist die Innenseite der Unterscheidung unmarkiert (n) und die Aussenseite der Unterscheidung markiert (m), dann ist der Wert der Gleichung unmarkiert (n).
- Ist die Innen- und Aussenseite der Unterscheidung unmarkiert (n), dann ist der Wert der Gleichung entweder unmarkiert (n) oder markiert (m).
Es fällt auf, dass bei einer Gleichung ersten Grades eine Wertbelegung vorkommen kann, die die Gleichung unbestimmbar macht. Im vierten Fall ist der Wert der Gleichung entweder unmarkiert (n) oder markiert (m).
Hinsichtlich einer Gleichung zweiten Grades – wir interpretieren sie als Zwei-Seiten-Formen mit Wiedereinführung – unterscheidet Spencer-Brown zwischen zwei Typen von Gleichungen.
Beim ersten Typ von Gleichungen zweiten Grades handelt es sich um selbstbestätigende bzw. tautologische Gleichungen. Die Wiedereinführung kann hier als positive Rückkopplung aufgefasst werden. Diese Gleichungen sind Gleichungen ersten Grades insofern ähnlich, als ihre Werte im vierten Fall ebenfalls entweder unmarkiert (n) oder markiert (m) sind.
Beim zweiten Typ von Gleichungen zweiten Grades handelt es sich um selbstverneinende bzw. paradoxe Gleichungen. Die Wiedereinführung kann hier als negative Rückkopplung aufgefasst werden. Diese Gleichungen unterscheiden sich von Gleichungen ersten Grades insofern, als ihre Werte im vierten Fall sowohl unmarkiert (n) als auch markiert (m) sind. Dies führt zu widersprüchlichen Ergebnissen (m=n oder n=m).
Mit Blick auf Zweit-Seiten-Form können wir also festhalten, dass die Wiedereinführung der Unterscheidung in das Unterschiedene zu einer Paradoxie führen kann: Das Markierte ist das Unmarkierte und umgekehrt ist das Unmarkierte das Markierte.
Um diese Paradoxie zu entfalten, führt Spencer-Brown neben der Dimension des Raums (Formen) die Dimension der Zeit in den Indikationenkalkül ein. Denn im Unterschied zum Treffen einer Unterscheidung, was wir als ein Ereignis auffassen können, handelt es sich bei der Wiedereinführung um einen Prozess, der Zeit in Anspruch nimmt. Spencer-Brown selbst vergleicht diesen Prozess mit der Durchquerung eines Tunnels, das von der einen Seite auf die andere Seite der Grenze der Unterscheidung führt (vgl. 2015: 48f).
Damit etabliert Spencer-Brown neben dem markierten und unmarkierten einen dritten Zustand, den imaginären Zustand. Er hebt die getroffene Unterscheidung innerhalb der Form insofern auf, als mit der Durchquerung des Tunnels ein Hin und Her zwischen den zwei Seiten möglich ist, ohne die ursprünglich getroffene Unterscheidung nachvollziehen zu müssen. Weil aber zwischen den zwei Seiten der getroffenen Unterscheidung ein untrennbarer Zusammenhang besteht, findet bei der Durchquerung des Tunnels jeweils gleichzeitig ein Wertwechsel statt.
Erst jetzt wird verständlich, weshalb Spencer-Brown im Zusammenhang mit dem 2. Axiom postuliert hat, dass wenn eine Absicht zur Überquerung und dann eine Absicht zur Rücküberquerung bestehe, der Wert der beiden Absichten zusammengenommen weder dem Wert des Inhalts auf der einen Seite (a) noch dem Wert des Inhalts auf der anderen Seite (b) entspreche.
In Abhängigkeit der Länge des Tunnels und der Geschwindigkeit bei dessen Durchquerung beginnt im imaginären Zustand die Unterscheidung zwischen ihren Werten (a, b) zu oszillieren. Damit verhindert Spencer-Brown einen Zusammenstoss zwischen gleichzeitig markierten und unmarkierten Werten und etabliert so ein stabiles System, das seine eigene Zeit generiert.
Die Oszillation ist eine typische Funktion von Gleichungen zweiten Grades des Typs paradoxe Gleichung. Sie löst Gleichungen bzw. Formen nicht als Kontradiktionen auf, sondern wechselt in Abhängigkeit der Zeit zwischen verschiedenen Aussagewerten (a, b, a, b, usw.) Demgegenüber weist Spencer-Brown Gleichungen zweiten Grades des Typs tautologische Gleichung eine Gedächtnisfunktion zu. Diese Gleichungen bzw. Formen führen über die Zeit hinweg zu den immer wieder gleichen Aussagewerten (a oder b).
^ ^ ^
Mit der Einführung der Äquivalenz (Gleichheitszeichen) wird die Voraussetzung dafür geschaffen, die Form der Unterscheidung in eine formale Sprache zu übersetzen.
˅ Formalisieren
Das Gleichheitszeichen, das in der klassischen Mathematik zwischen zwei wertgleichen Ausdrücken steht, verändert im Indikationenkalkül seine Bedeutung. Spencer-Brown schreibt im zweiten Kapitel der LoF: «Call expressions oft he same value equivalent» (2015: 4).
Im Indikationenkalkül steht das Zeichen also nicht für eine Identität zwischen zwei wertgleichen Ausdrücken, sondern für eine Äquivalenz derselben: Das, was in Abb. 1 auf der rechten Seite des Gleichheitszeichens steht, gleicht dem Wert nach dem, was auf der linken Seite steht. Die Ausdrücke auf der rechten und linken Seite der Gleichung sind aber offensichtlich nicht identisch.
Mit der Einführung der Äquivalenz ist die Voraussetzung dafür geschaffen, die Form der Unterscheidung in eine formale Sprache zu übersetzen. So ist der mit der Überquerung der Grenze («crossing») identifizierte Wert des Inhalts (Variable a) in der markierten Seite der Unterscheidung auf der rechten Seite der Gleichung äquivalent mit dem durch die Nennung des Namens («calling») identifizierten Wert (a) auf der linken Seit der Gleichung.
Oder: Der mit dem erneuten Überqueren der Grenze («recrossing») identifizierte Wert des Inhalts (Variable b) in der unmarkierten Seite der Unterscheidung auf der rechten Seite der Gleichung ist äquivalent mit dem durch die Nennung des Namens («calling») identifizierten Wert (b) auf der linken Seite der Gleichung.
Wir sehen an diesen Beispielen, dass Gleichungen immer von rechts nach links gelesen werden. Auf der rechten Seite steht der bestimmende und auf der linken Seite der zu bestimmende Wert der Gleichung.
^ ^ ^
Wir haben bis hierher versucht, die formale Sprache und das Notationssystem des Indikationenkalküls von Spencer-Brown nachzuvollziehen. Mit Fokus auf die Zwei-Seiten-Form haben wir dabei die primäre Arithmetik und Algebra weitgehend ausser Acht gelassen.
Vielmehr geht es an dieser Stelle darum, Bezugspunkte zwischen den LoF und der soziologischen Systemtheorie aufzuzeigen. Dabei fällt auf, dass sich Luhmann in erster Linie auf die basale Operation des Unterscheidens und die Zwei-Seiten-Form bezieht, während Baecker mit seinen «Katjekten» mit ineinander geschachtelten Unterscheidungen arbeiten (vgl. Baecker 2021).
Die vermeintliche Einverleibung des differenztheoretischen Ansatzes von Spencer-Brown in die Systemtheorie wird nicht unkritisch kommentiert. So kommen Peter Fuchs und Franz Hoegl in ihrem Aufsatz «Die Schrift der Form» zum Schluss, dass «Luhmann die Laws of Form als Thesaurus für brauchbare Metaphern nutzt und nicht: als Kalkül, nicht als Möglichkeit, soziologische Theorie zu formalisieren» (2015: 31).
Boris Hennig hat sich in seinem Aufsatz «Luhmann und die Formale Mathematik» die Mühe gemacht, die Fussnoten bezüglich Spencer-Brown in Luhmanns Werk mit den LoF zu vergleichen. Sein Fazit: «Das meiste nämlich, was Luhmann den Laws of form angeblich entnimmt, steht auf den zweiten Blick gar nicht darin» (2000: 157).
Vermutlich ging es Luhmann weniger darum, Spencer-Brown korrekt zu interpretieren und konsistent in sein Theoriegebäude zu integrieren. Vermutlich ging es ihm mehr darum, die Systemtheorie auf ein differenztheoretisches Fundament abzustellen und sich dabei der Sprache und des Notationssystems von Spencer-Brown zu bedienen, um sich selbst vom Resultaten überraschen zu lassen. «Man publiziert», hielt Luhmann einst fest, «nicht um zu belehren, sondern um beobachtet zu werden.» Und – möchte man hinzufügen – um sich selbst zu beobachten.
Polykontexturalität
Beobachten
Bei der Einführung des Beobachters bzw. der Beobachtung in seine Theorie verwendet Niklas Luhmann eine Reihe von Unterscheidungen, die er mit dem Anspruch getroffen hat, eine eigenständige Erkenntnistheorie für die soziologische Systemtheorie zu entwickeln. Dabei bricht er mit vielen Voraussetzungen der klassischen Erkenntnistheorie. Er begründet dies mit der Aussicht, neue Einsichten über soziale Systeme zu gewinnen.
Im Folgenden wollen wir die wichtigsten Unterscheidungen seiner Beobachtungstheorie kurz zusammenfassen.
˅ Operation und Beobachtung
Bevor wir auf die Unterscheidung von Operation und Beobachtung eingehen, müssen wir die Unterscheidung von Beobachter und Beobachten einführen. Wir werden im nächsten Abschnitt näher auf diese Unterscheidung eingehen. Gemäss der Systemtheorie ist ein Beobachter ein autopoietisches System und Beobachten eine Operation eines solchen Systems. Diese verkürzten Definitionen sollen vorerst ausreichen.
In der Systemtheorie bedeutet Operation die Reproduktion der Elemente eines Systems durch die Elemente desselben Systems. Diese Autopoiesis ermöglicht es, dass fortlaufend neue Operationen an vorangegangene Operationen anschliessen und somit das System am Laufen gehalten wird. Bei sinnprozessierenden Systemen wird zwischen psychischen und sozialen Systemen unterschieden. Die Form der Operation, das sich reproduzierende Element, ist bei Ersteren der Gedanke und bei Letzteren die Kommunikation.
Mit dem Begriff der Beobachtung schliesst die Systemtheorie an der Zweit-Seiten-Form von George Spencer-Brown an. Eine Beobachtung meint das Handhaben einer Unterscheidung zur Bezeichnung der einen und nicht der anderen Seite der Unterscheidung. Die Beobachtung bezieht sich also auf eine Referenz, auf etwas Bezeichnetes, und muss von der Operation, die referiert, unterschieden werden.
Das enge Verhältnis zwischen Operation und Beobachtung dekomponiert Luhmann in «Die Wissenschaft der Gesellschaft» genauer. Dabei geht es nicht um ein hierarchisches Verhältnis zwischen den zwei Begriffen, sondern um verschiedene Hinsichten auf die Unterscheidung von Operation und Beobachtung. Luhmann betont denn auch, dass es sich bei dieser Unterscheidung um eine rein funktionale, und nicht – im transzendentaltheoretischen Sinne – um eine ontologische Unterscheidung handle (vgl. 1990: 76).
Die Notwendigkeit, zwischen Operation und Beobachtung zu unterscheiden, erklärt Luhmann damit, dass beim Beobachten die verwendete Unterscheidung – gemeint ist die Form der Beobachtung – für den Beobachter selbst blind ist (vgl. ebd.: 115). Der Beobachter kann nicht in einem Zug die Operation des Beobachtens vollziehen und dabei noch die verwendete Unterscheidung beobachten.
Mit anderen Worten: Die Operation des Beobachtens kann nicht auf sich selbst angewandt werden. Darin liegt eine Form von Paradoxie, die durch Zeit entfaltet werden kann. Wollte der Beobachter sich selbst beim Beobachten beobachten, so würde dies eine weitere Beobachtung und damit Zeit erfordern.
«Das Problem», so Luhmann, «liegt also in der Zeit, und auch die Lösung liegt in der Zeit. Als Operation kann die Beobachtung sich nur momenthaft aktualisieren. Sie muss etwas bezeichnen […]. Das erzwingt den Verzicht auf Selbstbeobachtung auf der Ebene der Einzeloperation. Das schliesst jedoch nicht aus, dass andere Operationen, sei es gleichzeitig, sei es vorher oder nachher, das Beobachten beobachten, die benutzten Unterscheidungen unterscheiden – sofern nur ein Netzwerk rekursiven Beobachtens, also ein System hergestellt werden kann» (ebd.).
Das Beobachten der Unterscheidung von Operation und Beobachtung ist in zwei Hinsichten mögliche (vgl. ebd.: 77).
Einerseits kann ein Beobachter eine Operation als Beobachten beobachten, indem er den operativen Vollzug des Beobachtens beobachtet. Beobachten ist immer eine empirisch beobachtbare Operation. Der Beobachter beobachtet, was bezeichnet bzw. referiert wird.
Die Beobachtung einer Operation als Beobachten ist insofern von epistemologischer Relevanz, als sich mit dem Vollzug der Operation die Realität eines Beobachters bzw. eines autopoietischen Systems konstituiert. Realität im systemtheoretischen Sinne bezieht sich also immer auf das Operieren autopoietischer Systeme, und nicht etwa auf eine unabhängig von Beobachtern existierende Welt.
Vor diesem Hintergrund ist auch das viel diskutierte Zitat, mit dem Luhmann in «Soziale Systeme» einführt, zu verstehen: «Die folgenden Überlegungen gehen davon aus, dass es Systeme gibt» (2018a: 30).
Andererseits kann ein Beobachter eine Operation als Beobachtung beobachten, indem er die verwendete Unterscheidung einer Beobachtung beobachtet. Er beobachtet, wie bezeichnet bzw. referiert wird.
Auch mit dem Beobachten von Operationen als Beobachtungen beobachten Beobachter immer nur Beobachtungen von Welt. Selbst wenn mehrere Beobachtungen von Beobachtern konvergieren, resultiert daraus keine Realitätsgewissheit, sondern nur die Gewissheit, dass Kommunikation stattgefunden hat. Mit dem Beobachten von Beobachtungen konstruieren beobachtende Systeme ihre Wirklichkeit (operativer Konstruktivismus), die sich wiederum von ihrer operativen Realität unterscheidet.
Nach Luhmann hat deshalb die Frage, ob ein Beobachter sich täuscht oder nicht, nichts mit dem operativen Vollzug seiner Beobachtungen zu tun. Die Antwort auf diese Frage setzt vielmehr ein weiteres Beobachtungsschema (z.B.: richtig/falsch) voraus, mit der die Beobachtung des Beobachters beobachtet werden kann: «Wenn er sich täuscht, täuscht er sich eben real» (1990.: 78).
Wenn wir im Weiteren von Realität sprechen, meinen wir Beobachtungen von Operationen als Beobachten, und wenn wir von Wirklichkeit sprechen, meinen wir Beobachtungen von Operationen als Beobachtungen.
^ ^ ^
˅ Beobachter und Beobachten
Wir greifen die oben eingeführte Unterscheidung von Beobachter und Beobachten auf und gehen im Folgenden näher auf sie ein.
In seiner «Einführung in die Systemtheorie» weist Luhmann mit Nachdruck darauf hin, dass es sich beim Beobachter nicht nur um Bewusstseinssysteme handle (vgl. 2020: 142). Er subsumiert unter dem Beobachterbegriff alle autopoietischen Systeme, die zur Gewinnung und Verarbeitung von Informationen auf Basis von Unterscheidungen operieren. Dazu zählen also auch Kommunikationssysteme. Mit Blick auf Betriebssysteme stellt sich für die nächste Gesellschaft die Frage, ob sie sich auf eine weitere Systemreferenz einzustellen hat.

Beobachter können wir auffassen als die Einheit der Differenz von Operation und Struktur.
Nach Luhmann ist Beobachtung als autopoietische Operation zu verstehen (vgl. 1990: 131). In sinnprozessierenden Systemen schliessen demnach neue Operationen des Beobachtens fortlaufend an vorangegangene Operationen des Beobachtens an. Aufgrund der Autopoiesis kommt es beim Beobachter zu einer operativen Schliessung und damit zu einer Abgrenzung von seiner Umwelt.
Da der operative Vollzug des Beobachtens eines Beobachters für andere Beobachter empirisch beobachtbar ist, erscheint er in der sozialen Welt als ein real existierendes System. Der Beobachter ist demnach ein Artefakt einer Zurechnung von Beobachtungen durch Beobachtungen.
Um ein fortlaufendes Beobachten sicherzustellen, muss der Beobachter ein strukturiertes System sein. Die Strukturen schränken ein, was der Beobachter beobachten kann. Sie bestimmen den Möglichkeitsspielraum verwendbarer Unterscheidungen und damit auch die Wirklichkeit des Beobachters.
Mit der internen Ausdifferenzierung von Strukturen unterscheidet sich der Beobachter von seiner Umwelt. Er markiert damit eine Grenze zu seiner Umwelt und bestimmt seine eigene Identität. «Beobachter», so Luhmann, «sind stets nur mit sich selbst identisch, weil sie über eine jeweils selbstgezogene Grenze beobachten, und andere Systeme können allenfalls Beobachter beobachten, wie sie beobachten, aber nicht an ihren Beobachtungen teilnehmen» (ebd: 79).
Während sich Realität auf den operativen Vollzug bezieht, bezieht sich Wirklichkeit auf die Konstruktion, den Erhalt und die Revision interner Strukturen. Wobei zwischen Strukturen (Wirklichkeitsbezug) und Operationen (Realitätsbezug) ein zeitlich rekursiver Zusammenhang besteht: Die Strukturen sinnprozessierender Systeme leiten deren Operationen, die die Strukturen wiederum entweder bestätigen oder revidieren.
Beobachten wiederum können wir als Einheit der Differenz von Unterscheiden und Bezeichnen auffassen.
Im Unterschied zu George Spencer-Brown verwendet Luhmann nicht den Begriff des Hinweisens («indication»), sondern den des Bezeichnens (vgl. ebd.: 79ff). Unterscheiden und Bezeichnen finden in einer und derselben Operation statt. Deshalb bring die Formulierung «unterscheidendes Bezeichnen» diese Operation präziser auf den Punkt.
Wie wir in der Diskussion der Zwei-Seiten-Form bereits gesehen haben, markiert ein Beobachter beim unterscheidenden Bezeichnen eine Grenze mit der Folge, dass zwei Seiten entstehen. Gleichzeitig bezeichnet er immer eine Seite der Grenze. Das Bezeichnen beider Seiten würde die getroffene Unterscheidung aufheben und also keinen Sinn ergeben. Deshalb sprechen wir mit Spencer-Brown immer von einer markierten Seite (m) und einer unmarkierten Seite (n) der Unterscheidung. Das bedeutet auch, selbst wenn die Form der Unterscheidung symmetrisch ist, kann ein Beobachter sie immer nur asymmetrisch verwenden.
Um von einer auf die andere Seite der Unterscheidung zu wechseln, muss der Beobachter die Grenze überschreiten («crossing»). Nach Luhmann beansprucht diese Operation Zeit. Zeit spielt in der Systemtheorie insofern eine zentrale Rolle, als sie nach Luhmann der Entparadoxierung von Paradoxien dient. Die Paradoxie, dass nicht beide Seiten einer Unterscheidung gleichzeitig bezeichnet werden können, löst die Zeit auf, indem sie dem Beobachter erlaubt, zwischen den zwei Seiten hin und her zu wechseln, um mal diese, mal die andere Seite bezeichnen zu können.
Beobachten als Unterscheiden und Bezeichnen ist für Luhmann ein Anwendungsfall einer viel allgemeineren Operationsweise, die der Evolution autopoietischer Systeme zugrunde liegt. Er bezeichnet diese Operationsweise als Überschussproduktion und Selektion (vgl. ebd.: 81f). Demnach produzieren autopoietische Systeme in ihrem operativen Vollzug immer mehr Möglichkeiten als sie tatsächlich verwenden können.
Mit Blick auf Kommunikationssysteme und Bewusstseinssysteme bedeutet dies, dass sich bei der Aktualisierung einer Kommunikation bzw. eines Gedankens immer weitere Möglichkeiten eröffnen, an denen nächste Kommunikationen bzw. Gedanken durch Selektion anschliessen können. In diesem Sinne produziert auch das Unterscheiden immer mehr Möglichkeiten als die, die dann tatsächlich bezeichnet wird.
Sinnprozessierende Systeme aktualisieren also laufend eine Unterscheidung und verweisen dabei immer auf andere Möglichkeiten mitgemeinter oder miterfasster Unterscheidungen. Deshalb meint Sinn immer sich selbst und einen mitgeführten Sinnüberschuss.
^ ^ ^
˅ Beobachtung und Differenz
Wie wir bei der Unterscheidung von Operation und Beobachtung gesehen haben, kann sich der Beobachter im Vollzug der Operation des Beobachtens nicht selbst beobachten. Er kann weder die von ihm verwendete Unterscheidung noch die durch sie erzeugte Differenz beobachten.
Eine Differenz bedeutet, dass sich innerhalb einer Unterscheidung die beiden Seiten der Unterscheidung durch unterschiedliche Werte unterscheiden. Wären sie gleichwertig, gäbe es kein Motiv, diese und nicht eine andere Unterscheidung zu treffen.
Und wie wir bei der Unterscheidung von Beobachter und Beobachten gesehen haben, entwickelt ein autopoietisches System interne Strukturen, um ein kontinuierliches Beobachten sicherzustellen und um Komplexität durch die Einschränkung möglicher Unterscheidungen zu reduzieren. Auf diese Weise konstruiert es eine eigene Identität vis-à-vis seiner Umwelt.
Die Ausdifferenzierung interner Strukturen ermöglicht zudem Beobachtungen, die sich auf die Identität des Beobachters bzw. auf die Einheit der Differenz von System und Umwelt beziehen. Diese Differenz wird als Unterscheidung wieder in das System eingeführt. Durch diese Reflexion gewinnt der Beobachter Orientierungswerte, die die interne Anschlussfähigkeit von Operationen und damit den Möglichkeitsspielraum von Unterscheidungen bestimmen (vgl. 1990: 83).

Peter Fuchs weist in seinem Büchlein «Der Sinn der Beobachtung» darauf hin, dass die Wiedereinführung der Differenz von System und Umwelt in das System als eine Art von Selbsterrechnung des Systems als einen imaginären Wert zu verstehen sei (vgl. 2015: 16f). Damit schliesst er an Spencer-Brown an, der neben dem markierten und dem unmarkierten Zustand einen dritten, nämlich den imaginären Zustand einer Unterscheidung vorgeschlagen hat.
Wie wir aus der Diskussion der Zwei-Seiten-Form wissen, beginnt die Unterscheidung im imaginären Zustand zwischen den beiden Seiten der Unterscheidung, in unserem Fall also zwischen System und Umwelt, zu oszillieren. Im Oszillieren etabliert und stabilisiert sich das System und erzeugt seine eigene Systemzeit.
Daraus folgt nach Fuchs, dass Bewusstseins- und Kommunikationssysteme, insofern sie als Beobachter beobachtet werden, weniger als eigenständige Entitäten zu verstehen sind, sondern vielmehr als Ausdruck imaginärer Werte aufzufassen sind, mit denen gerechnet werden kann. In diesem Sinne kann der Beobachter – wie oben bereits erwähnt – als ein Artefakt einer Zurechnung von Beobachtungen durch Beobachtungen verstanden werden.
Da System und Umwelt eine Einheit bilden, kann man sie nicht separat beobachten, ohne in die klassische Semantik der Ontologie zurückzufallen: «Wird auf die Rückversicherung in Ontologie verzichtet, bleibt das System als Differenz. Es ist (wie jede Differenz) kein Ding, kein Subjekt, kein Objekt, keine Festigkeit. Ausser für einen Beobachter ist es: nichts. Systeme […] entziehen sich deshalb der Wahrnehmung. Noch nie hat jemand ein System gesehen. Der Ausdruck ‹Unjekt› steht für dieses Problem» (ebd.)
^ ^ ^
˅ Beobachtungen erster und zweiter Ordnung
Vor dem Hintergrund der bisherigen Ausführungen können wir nun die Beobachtungsverhältnisse genauer bestimmen.

Bei der Beobachtung erster Ordnung macht ein Beobachter einen Unterschied, indem er eine Unterscheidung wählt und auf die markierte Innenseite hinweist. Es handelt sich dabei um den operativen Vollzug des Beobachtens.
Wie aus der Diskussion der Zwei-Seiten-Form bekannt, besteht ein vollkommener Zusammenhang zwischen der markierten Innenseite (m) und der unmarkierten Aussenseite (n) einer Unterscheidung. Obwohl die unmarkierte Aussenseite konstitutiv für die Unterscheidung ist, stellt sie für den Beobachter einen sogenannten blinden Fleck dar. Der Beobachter kann im Moment des operativen Vollzugs des Beobachtens nicht gleichzeitig auf beide Seiten der Unterscheidung hinweisen. Luhmann bringt diesen Sachverhalt auf die Formel: «Es (das Beobachten, Anm. CMS) kann nur sehen, was es mit dieser Unterscheidung sehen kann. Es kann nicht sehen, was es nicht sehen kann» (1990: 85).
Die Beobachtung erster Ordnung nimmt immer die Unterscheidung der Form in den Blick, die aus einer Grenze, der markierten Innenseite (m) und der blind mitlaufenden unmarkierten Aussenseite (n) besteht.
Bei der Beobachtung zweiter Ordnung beobachtet ein Beobachter mit Hilfe einer anderen Unterscheidung eine Beobachtung erster Ordnung, indem er auf sie hinweist und ihre Differenz thematisiert. Dies ist bei der Beobachtung erster Ordnung nicht möglich. Daher kann nur eine Beobachtung zweiter Ordnung den blinden Fleck einer Beobachtung erster Ordnung sichtbar machen.
Wie wir ebenfalls aus der Diskussion der Zwei-Seiten-Form wissen, markiert eine Unterscheidung ihrerseits eine Grenze innerhalb des Möglichkeitsspielraums anderer Unterscheidungen. Deshalb kann die Aussenseite der Unterscheidung auch als unmarkiert (n) ausgezeichnet werden.
Beobachtet nun ein Beobachter mit Hilfe einer aus dem Möglichkeitsspielraum von Unterscheidungen gewählten Unterscheidung eine Beobachtung erster Ordnung, dann verfügt auch die Beobachtung zweiter Ordnung über einen blinden Fleck. Luhmann bezeichnet diesen Sachverhalt mit dem Begriff der operativen Naivität des Beobachtens: «[…] man kann auch sagen, dass alles Beobachten, auch das Beobachten von Beobachtungen, auf der operativen Ebene naiv verfährt; oder mit nochmals anderen Worten: dass es in Bezug auf die eigene Referenz unkritisch vergeht» (ebd.)
Eine Beobachtung zweiter Ordnung kann entweder aus einer selbstreferenziellen Perspektive (Selbstbeobachtung) oder aus einer fremdreferenziellen Perspektive (Fremdbeobachtung) erfolgen. In letzterem Fall ist die Fremdbeobachtung nur unter Rückgriff auf eigene Beobachtungen bzw. Unterscheidungen möglich. Beobachtungen zweiter Ordnungen sind immer rekursive Operationen, weil sie sich auf vorangegangene Beobachtungen erster Ordnung beziehen.
Die Beobachtung zweiter Ordnung nimmt mit Hilfe einer anderen Unterscheidung immer die Form der Unterscheidung der Beobachtung erster Ordnung in den Blick, die aus einer Grenze, der markierten Innenseite (m) und der unmarkierten Aussenseite (n) sowie der blind mitlaufenden anderen Formen der Unterscheidung (n) besteht.
Bei der Reflexion handelt es sich um einen Spezialfall der Selbstbeobachtung. Wie wir bei der Unterscheidung von Beobachtung und Differenz gesehen haben, ermöglicht die Ausdifferenzierung interner Strukturen dem Beobachter Beobachtungen durchzuführen, die sich auf seine Identität bzw. auf die Einheit der Differenz von System und Umwelt beziehen.
Die Reflexion kommt durch eine Wiedereinführung der Unterscheidung der Form in die Form der Unterscheidung zustande. Das bedeutet, dass die Operation der Wiedereinführung eine Unterscheidung aus einer doppelten Perspektive verwendet. Die Unterscheidung der Form weist als Beobachtung erster Ordnung auf eine aktuell markierte Seite hin. Und die Form der Unterscheidung nimmt als Beobachtung zweiter Ordnung beide Seiten der Unterscheidung in den Blick. Die Wiedereinführung der aktuellen Unterscheidung in die Form der Unterscheidung ermöglicht die Beobachtung, wie die aktuelle Unterscheidung durchgeführt wird.
Erst diese dritte Möglichkeit, die Reflexion, erlaubt es einem System, zwischen Unterscheidungen, die sich nicht auf die Unterscheidung von System und Umwelt beziehen, und Unterscheidungen, die die Unterscheidung von System und Umwelt durchführen, zu unterscheiden. Erst mit dieser speziellen Art der Selbstbeobachtung kann das System eine Grenze ziehen und sich selbst als Einheit bezeichnen – eine Einheit, die sich in sich selbst von sich selbst unterscheiden kann und sich selbst von seiner Umwelt.
^ ^ ^
Sinn
Sinn ist nach Niklas Luhmann eine unhintergehbare Voraussetzung des Erlebens und Handelns. Er bildet das Universalmedium, in dem psychische Systeme mittels Gedanken und soziale Systeme mittels Kommunikation operieren. Als gemeinsame Errungenschaft ist Sinn auf dem Wege der Koevolution psychischer und sozialer Systeme entstanden.
Sinn ist also nichts, was in der Welt gegeben ist. Weder Subjekte noch Objekte sind Träger von Sinn. Sinn wird produziert und reproduziert durch psychische und soziale Systeme. Würden sie aufhören, Sinn zu prozessieren, verschwände Sinn aus der Welt und mit ihm der Weltbegriff selbst.
Luhmann nähert sich dem Sinnbegriff aus verschiedenen theoretischen Perspektiven, die im Folgenden kurz skizziert werden (vgl. 2018a: 98ff, 2015: 44ff).
˅ Sinn als Einheit
Luhmann definiert Begriffe mit Hilfe der Zwei-Seiten-Form durch unterscheidendes Bezeichnen, beispielsweise: x bedeutet dies und nichts anderes. Damit gewinnt der einzelne Begriff im Kontext anderer möglicher Unterscheidungen an Schärfe. Wie aber verhält es sich mit dem unterscheidenden Bezeichnen hinsichtlich des Sinnbegriffs?
Nach Luhmann bildet der Sinnbegriff eine Ausnahme. Denn er ist unnegierbar: Wollte man Sinn sprachlich negieren, müsste man dazu Sinn beanspruchen. «Sinn», so Luhmann, «ist also eine unnegierbare, eine differenzlose Kategorie» (2018a: 96).
Wenn Sinn sich in der Zwei-Seiten-Form nicht von der unmarkierten Aussenseite her bestimmen lässt, wie gewinnt der Begriff dennoch an Schärfe? Luhmann wählt den Weg, die markierte Innenseite der Unterscheidung, den Sinn, weiter auszudifferenzieren. Der Sinnbegriff bestimmt sich also durch Binnendifferenzierungen.
^ ^ ^
˅ Sinn als Differenz
Im Anschluss an Edmund Husserls Phänomenologie nimmt Luhmann eine erste Binnendifferenzierung vor und führt die Unterscheidung zwischen Aktualität und Möglichkeit ein.

Psychische Systeme prozessieren Sinn immer intentional. Sie richten ihre Gedanken auf etwas Bestimmtes und schliessen dabei mögliche andere Bestimmtheiten aus. Analoges gilt für soziale Systeme. In jeder Kommunikation wird etwas Bestimmtes thematisiert, während Anderes im Horizont der Möglichkeiten bleibt. Sinnprozessierende Systeme aktualisieren also laufend Bestimmtes und verweisen dabei immer auf andere Möglichkeiten mitgemeinter oder miterfasster Bestimmtheiten. Deshalb meint Sinn immer sich selbst und einen mitgeführten Sinnüberschuss.
Sinnüberschuss, so Dirk Baecker in seinem Aufsatz «Niklas Luhmann und die Kultursoziologie», meint, «dass in jeder Situation, in der ein bestimmter Sinn in Anspruch genommen wird, an dem sich eine Handlung oder eine Kommunikation orientiert, der Sinn anderer Situationen alternativ zur Verfügung steht und auf irgendeine Art und Weise, sei es annehmend oder ablehnend, berücksichtigt werden muss» (2019a: 6).
Aus dieser Binnendifferenzierung ergibt sich die Sinnform1, nämlich die Einheit der Differenz von Aktualität und Möglichkeit.
Mit Blick auf die Differenztheorie hält Luhmann zudem fest, dass die Operationsfähigkeit von Sinn nur durch die Wiedereinführung der Sinnform in die Sinnform gegeben ist. Das bedeutet, dass eine aktuelle Bestimmtheit aufnahmefähig sein muss für die jeweils getroffene Unterscheidung zwischen Aktualität (Sinn) und Möglichkeit (Sinnüberschuss). Diese Aufnahmefähigkeit erlaubt es, die Anschlussmöglichkeiten nächster Sinnformen vorzuselektionieren. «Auf diese Weise», so Luhmann, «wird Sinn zu einem sich selbst laufend regenerierenden Medium für die laufende Selektion bestimmter Formen» (2015: 58).
^ ^ ^
˅ Sinn als Medium und Form
Im Anschluss an Fritz Heiders Untersuchungen über Wahrnehmungsmedien nimmt Luhmann eine zweite Binnendifferenzierung vor und führt die Unterscheidung zwischen Medium und Form ein (vgl. 2015: 190ff).

Ein Medium besteht nach Luhmann aus einer losen gekoppelten Menge von bestimmten Elementen, die sich nach bestimmten Selektionen zu strikt gekoppelten Elementen verknüpfen lassen und damit eine Form bilden. Wobei das Medium qua Medium die möglichen Selektionen immer schon limitiert, um die Beliebigkeit von Verknüpfungen einzuschränken. Gleichzeitig aber weitet es die Selektionsmöglichkeiten aus, weil es Formen vorschlägt und die Bildung von Formen anregt. Es ist also gleichzeitig eine Schliessung von und eine Öffnung für Selektionen.
Aus der zweiten Binnendifferenzierung ergibt sich die Sinnform2, nämlich die Einheit der Differenz von Medium und Form.
So erlaubt beispielsweise die lose gekoppelte Menge von Worten unter Einhaltung der Regeln der Syntax die verständliche Formulierung von ganzen Sätzen. Nicht unwichtig dabei ist, dass sich im Verlauf der Zeit der Gebrauch des Mediums und damit auch die Anwendung der Selektionsregeln – in unseren Beispielen der Syntax – verändern können.
Das Beispiel der natürlichen Sprache weist auf zentrale Aspekte der Unterscheidung von Medium und Form hin. Erstens – und das ist typische für Unterscheidungen in Zwei-Seiten-Formen – bedingen sich Medium und Form gegenseitig. Ein Medium ist nicht ohne seine Formen und Formen sind nicht ohne ihr Medium denkbar. Ohne Worte, keine Sätze. Und ohne Sätze, keine Worte.
Zudem teilen sich Medium und Form dieselben Elemente, beispielsweise Worte. Luhmann spricht in diesem Zusammenhang auch von «medialem Substrat». Der Unterschied zwischen Medium und Form besteht allein in Bezug auf die Art der Kopplung, lose oder strikte Kopplung.
Weiter lassen sich die Elemente eines medialen Substrats als Formen eines ihm zugrundeliegenden einfacheren Mediums interpretieren. So können Worte im Medium der mündlichen Sprache als mediales Substrat und im Medium der Lautlichkeit als Form aufgefasst werden. Und umgekehrt können die Formen eines Mediums als mediales Substrat eines höherstufigen Mediums fungieren. So bilden die Sätze als Formen der mündlichen Sprache das mediale Substrat im Medium der Rede.
Auch sind Formen flüchtig und instabil, während das Medium dauerhaft und stabil ist. Dies zeigt sich typischerweise am Medium der mündlichen Sprache. Einmal ausgesprochene Sätze verhallen nur allzu schnell, während die unausgesprochenen Worte von dauerhaftem Bestand sind.
Sodann manifestiert sich der Gebrauch eines Mediums in einem Prozess des Koppelns und Entkoppelns. Psychische Systeme richten ihre Gedanken bald auf dies, bald auf jenes. Und soziale Systeme thematisieren in Kommunikationen mal dies, mal das.
Schliesslich zeichnet sich das Medium durch einen unsichtbaren, virtuellen Charakter aus. Medium ist unbestimmte Potenzialität. Diese wird erst durch Formbildung temporär aktualisiert und wahrnehmbar. Form ist demnach bestimmte Aktualität. Beispielsweise werden in der mündlichen Sprache nicht die einzelnen, rasch über die Lippen purzelnden Worte (Medium), sondern vielmehr der temporär aktualisierte Sinn der Sätze (Formen) verstanden.
^ ^ ^
˅ Sinndimensionen
Wie wir bei der Bestimmung von Sinn als Differenz von Aktualität und Möglichkeit gesehen haben, aktualisieren sinnprozessierende Systeme etwas Bestimmtes und verweisen dabei immer auf andere Möglichkeiten mitgemeinter oder miterfasster Bestimmtheiten. Dieser Sinnüberschuss lässt sich in drei Dimensionen unterscheiden.
Die Verweisung auf andere sachliche Sinngehalte (Sachdimension), die Verweisung auf Vergangenes oder Künftiges (Zeitdimension) und die Verweisung auf andere Personen (Sozialdimension).
^ ^ ^
Sein
Ontologie ist für Niklas Luhmann eine historisch determinierte Kategorie der Vormoderne, die aufgegeben werden sollte, weil sie mit der Kontingenz und Komplexität der modernen Gesellschaft nicht vereinbar ist.
Die im 16. Jahrhundert aufkommende Rede von «Ontologie» markiert nach Luhmann eine Krise, die mit dem Leitmedienwechsel von der Schrift zum Buchdruck einherging und den Übergang von der vormodernen zur modernen Gesellschaft begleitete. Garantierten in der Vormoderne gemeinsam geteilte ontologische Annahmen eine einheitliche Weltsicht und gefestigte Gesellschaftsstruktur, so machte der Buchdruck heterogene Weltbeschreibungen sichtbar und setzte Kritik an der stratifikatorischen Gesellschaftsstruktur frei. Angesichts dieser Unruhen brauchte es den Ontologiebegriff, um das, was bis dahin selbstverständlich war, zu bezeichnen. Ontologie bedeutete die Lehre vom Seienden.
˅ De-Ontologisierung
In «Gesellschaft der Gesellschaft» setzt sich Niklas Luhmann kursorisch mit dem Begriff der Ontologie auseinander (vgl. 2015: 893ff). Er beleuchtet ihn aus einer wissenssoziologischen und aus einer erkenntnistheoretischen Perspektive.
Die Differenzierungsform, die nach Luhmann die Beschreibung von Welt und Gesellschaft in der Vormoderne dominierte, war die soziale Schichtung sowie die Unterscheidung von Zentrum und Peripherie. Der Adel bildete die Spitze und die Städte die Zentren einer homogenen, hierarchisch strukturierten Gesellschaft. Die vorherrschende Welteinstellung war die Ontologie. Sie dirigierte die Selbstbeobachtung und Selbstbeschreibung der Vormoderne. Was aber bedeutet Ontologie in diesem historischen Kontext?

«Als Ontologie», so Luhmann, «wollen wir das Resultat einer Beobachtungsweise bezeichnen, die von der Unterscheidung Sein/Nichtsein ausgeht und alle anderen Unterscheidungen dieser Unterscheidung nachordnet» (ebd.: 895). Die Unterscheidung beruht auf der plausiblen Annahme, dass nur das Sein ist und das Nichtsein nicht ist. In der Sprache der klassischen Logik heisst das: tertium non datur.
So hält schon Platon in seinem «Der Staat» in einem Dialog fest: «Der Erkennende, erkennt er etwas oder nichts? […] – Ich werde antworten, sagte er, dass er etwas erkennt. – Was ist, oder was ist nicht? – Was ist; denn wie könnte etwas, was ja nicht ist, erkannt werden? – Dies also wissen wir zur Genüge, und wenn wir es von noch soviel Seiten betrachteten, dass das vollkommen Seiende auch vollkommen erkennbar ist, das auf keine Weise Seiende aber auch ganz und gar unerkennbar. – Vollkommen zur Genüge» (476 e f).
In der Definition des Seins zeigt sich eine interessante Parallele zur Definition des Sinns. Wie der Sinn den Unsinn, so schliesst das Sein das Nichts in die Unterscheidung mit ein. Und doch bleibt beides, Unsinn und Nichts, ausgeschlossen. Das Sein ist wie der Sinn eine unnegierbare, eine differenzlose Kategorie. Die Ausdifferenzierung von Welterkenntnis vollzieht sich deshalb ausschliesslich auf der markierten Innenseite der Unterscheidung, also im Sein. Es wird mit fortschreitendem Erkenntnisgewinn immer weiter aufgelöst und eingeteilt in Kategorien, in Arten und Gattungen.
Diese Besonderheit der Binnendifferenzierungen führt dazu, dass die Zwei-Seiten-Form der Einheit der Differenz von Sein und Nichtsein asymmetrisch ist. Wenn man die Grenze von Sein und Nichtsein kreuzt und wieder zurückkehrt, dann bringt man keinen Erkenntnisgewinn zurück. Gleichwohl hält Luhmann fest: «Das Nichtsein ist ein notwendiges Implikat der Beobachtung des Seins» (ebd.: 898).
Bei der Beobachtung, bei der Unterscheidung von Sein und Nichtsein, kann es jedoch zu Verwechslungen kommen. Diese Verwechslungen können beispielsweise bei der Verwendung von Sprache auftreten, in der Zeichen eine Art Stellvertreterfunktion übernehmen. Zeichen stehen immer für etwas, ohne dieses Etwas selbst zu sein. So kann es vorkommen, dass ein Zeichen etwas bezeichnet, was es nicht ist oder nicht sein kann.
Um diese Verwechslungsgefahr zu vermeiden, schliesst die Unterscheidung von Sein und Nichtsein ein quasi normatives Postulat mit ein: Es existiert nur, was existieren soll. Folglich hat ein Beobachter erster Ordnung mit seinen Ist-Aussagen die Welt und Gesellschaft möglichst akkurat zu beschreiben. Das Sein und seine Ordnung dürfen dabei nicht infrage gestellt werden.
Wenn in Kommunikationen dennoch unterschiedliche Unterscheidungen über Welt und Gesellschaft zirkulieren, dann bedarf es einer Instanz, die die normative Kraft der geteilten ontologischen Annahmen durchsetzen kann. Luhmann nennt hierfür zwei Kandidaten: Gott und Logik.
Gott liegt ausserhalb der ersten Unterscheidung von Sein und Nichtsein. Als Einheit des Ursprungs ist er das erste Prinzip. Er hat für den Menschen eine Welt der Unterscheidungen geschaffen, ohne selbst in ihr unterscheidbar zu sein. Gott steht für die transzendente Garantie der Unverletzbarkeit des Seins. Mit anderen Worten: Nur Gott kann auf wundersame Weise die erste Unterscheidung von Sein und Nichtsein aufheben und damit seine Existenz beweisen.
Logik steht für die immanente, weltliche Garantie der Unverletzbarkeit des Seins. Ihr Ursprung liegt in kommunikativen Problemen. Obwohl Beobachter erster Ordnung in ihren Aussagen über dasselbe Seiende übereinstimmen sollten, gelangen sie immer wieder zu abweichenden Meinungen. Dieser Sachverhalt wurde bereits in der Antike anhand der Unterscheidung von Wissen («epistéme») und Meinung («dóxa») diskutiert.
Um die Unterscheidung von Wissen und Meinung handhabbar zu machen, muss das Beobachten selbst thematisiert werden. Dazu wird zum einen die Unterscheidung von Sein und Denken eingeführt, die erst eine Ausdifferenzierung von Logik ermöglicht. Und zum anderen wird die Beobachtung zweiter Ordnung eingeführt, mit der die logische Konsistenz der Wahrheitsansprüche von Beobachtungen erster Ordnung überprüft werden können. Die Funktion der Logik ist es also, Irrtümer zu korrigieren, die dadurch entstehen, dass Beobachter etwas für wahr halten, was nicht wahr ist, oder umgekehrt.
Der vormoderne Begriff der Ontologie sollte die Funktion erfüllen, mit Hilfe der ersten Unterscheidung von Sein und Nichtsein die zunehmenden Einwände gegen die Einheit von Welt und Gesellschaft zu verteidigen. Diese Strategie ist nach Luhmann in der modernen, funktional differenzierten Gesellschaft nicht mehr haltbar. Deshalb braucht es eine neue erste Unterscheidung, aus der neue Formen der Selbstbeobachtung- und Selbstbeschreibung hervorgehen können.
Luhmann kritisiert am Ontologiebegriff, dass er die Unterscheidung von Sein und Nichtsein als erste Unterscheidung voraussetzt und ihr alle weiteren Unterscheidungen unterordnet. Die Unterscheidung von Sein und Nichtsein ist aber nur ein Beobachtungsschema unter vielen möglichen Schemata. Damit solche Beobachtungsschemata überhaupt zur Anwendung kommen können, bedarf es der vorgängigen Unterscheidung von Beobachter und Beobachtetem. Luhmann plädiert daher mit Spencer-Brown für das Primat der Beobachtung als erster Unterscheidung.
«Radikalisiert man aber das Konzept des unterscheidungsabhängigen Beobachtens», so Luhmann, «findet man sich in einer anderen Welt» (ebd.: 910).
Es handelt sich hierbei um eine Welt, in der von Einheit, dem Sein, auf Differenz, Selbstreferenz und Fremdreferenz, umgestellt worden ist.
^ ^ ^
Trotz der De-Ontologisierung kommt Luhmann nicht umhin, für die Beschreibung der modernen Gesellschaft eine Minimalontologie zu verwenden, die aus Beobachter und Beobachtung besteht.
Zu den Beobachtern zählt Luhmann psychische und soziale Systeme. Peter Fuchs weist darauf hin, dass wir auch ihnen keinen ontologischen Status im Sinne von Substanz zuschreiben sollten. Wer ist schon mal mit einem psychischen oder sozialen System in Berührung gekommen? Bei Beobachtern handelt es sich vielmehr um funktionale Zurechnungspunkte von Beobachtungen im Kommunikationsprozess und damit um imaginäre Werte (vgl. Fuchs 2015). Unter Beobachtungen versteht Luhmann die Operation des Unterscheidens und Bezeichnens psychischer und sozialer Systeme.
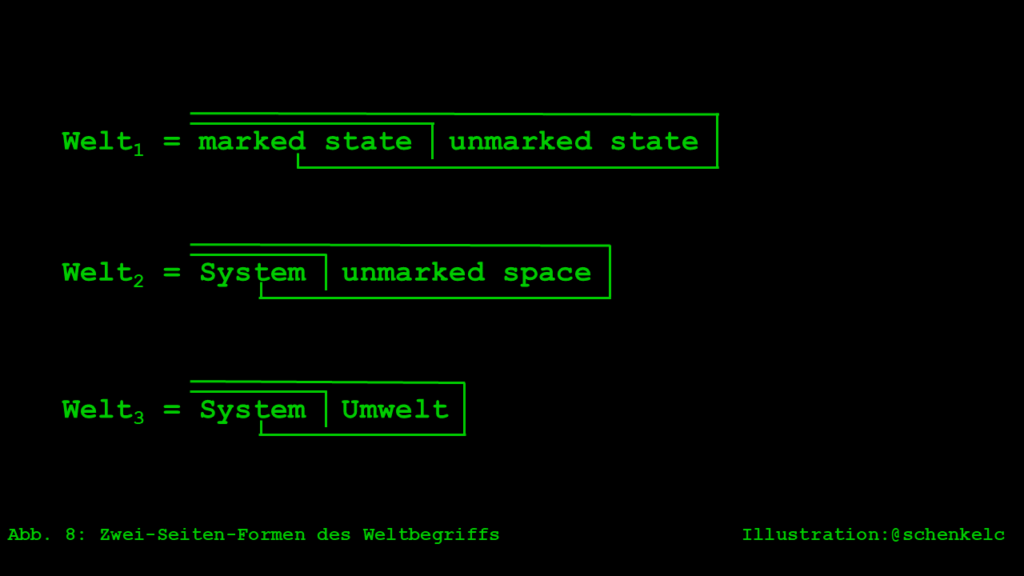
Wenn wir mit dieser Minimalontologie, Beobachter und Beobachtung, auf Luhmanns systemtheoretischen Weltbegriff schauen, so können wir dies aus drei Perspektiven tun: aus einer phänomenologischen (Welt1), einer differenztheoretischen (Welt2) und einer medientheoretischen (Welt3). Diese drei Perspektiven auf den Weltbegriff sind rein analytisch, beim Prozessieren von Sinn durch psychische und soziale Systeme bilden sie immer eine Einheit (Welt).
Der Begriff der Welt1, Welt als Einheit der Möglichkeiten, beschreibt einen «unmarked state», einen unterscheidungslosen Weltzustand. Dieser Zustand wird erst durch das Auftreten eines Beobachters, der im Medium des Sinns operiert, verändert. Sinn und Welt sind nach Luhmann eng miteinander verbunden: Beide sind unausweichlich, differenzlos und in jeder Sinnform als Verweis auf die Gesamtheit aller Möglichkeiten enthalten.
˅ Welt als Einheit der Möglichkeit
Phänomenologisch müssen wir uns Luhmanns Weltbegriff W1 ohne Beobachter und ohne Beobachtungen vorstellen. Es handelt sich dabei um den unterscheidungslosen Weltzustand.
In Anlehnung an Spencer-Brown nennt Luhmann diesen Zustand der Welt1 «unmarked state» (vgl. 1990: 93, 262, 1995a: 51 f., 1997: 49). In «Die Kunst der Gesellschaft» führt er ihn mit folgenden Worten ein: «Der Begriff der Form […] setzt deshalb die Welt als ‹unmarked state› voraus. Die Einheit der Welt ist unerreichbar, sie ist weder Summe, noch Aggregat, noch Geist. Wenn eine neue Operationsreihe mit einer Differenz beginnt, die sie selber macht, beginnt sie mit einem blinden Fleck. Sie steigt aus dem ‹unmarked state›, in dem nichts zu sehen ist und nicht einmal von ‹Raum› gesprochen werden könnte, in den ‹marked state› ein, und zieht, indem sie sie überschreitet, eine Grenze. Die Markierung erzeugt den Raum der Unterscheidung, die Differenz von ‹marked space› und ‹unmarked space›» (1995a: 51). Anzumerken ist, dass Luhmann in einer Fussnote zu diesem Zitat darauf hinweist, dass Spencer-Brown selbst nur zwischen «marked space» und «unmarked space» unterschieden hat (vgl. ebd.: Fn. 63).
Die Unversehrtheit des Welt1 wird also erst durch das Auftreten des Beobachters verletzt. Nach Luhmann kann grundsätzlich davon ausgegangen werden, «dass die Welt (was immer das ist) das Unterscheiden toleriert […]» (1990: 93). Beobachter beobachten immer im Universalmedium des Sinns. Die Welt1 muss also die Voraussetzungen für die Möglichkeit des Prozessierens von Sinn schaffen.
Sinn verweist immer auf weiteren Sinn. Indem Beobachter Sinn prozessieren, aktualisieren sie fortwährend bestimmte Sinnformen und verweisen zugleich auf mögliche andere Sinnformen. «Die zirkuläre Geschlossenheit dieser Verweisungen», schreibt Luhmann in «Soziale Systeme», «erscheint in ihrer Einheit als Letzthorizont alles Sinnes: die Welt» (1984: 105). Welt ist demnach die Summe und die Einheit aller Möglichkeiten sinnhafter Verweisungen. Oder mit einem Begriff aus «Die Gesellschaft der Gesellschaft» können wir Welt auch als «virtuelle Realität» verstehen (1997: 47).
Die Einheit der Differenz von Sinn und Welt ist für Luhmann die letztgültige Form für eine Weltbeschreibung. Sie verweist auf eine spezifische Ähnlichkeit des Sinn- und Weltbegriffs. Beide sind unausweichlich und unnegierbar.
Unausweichlichkeit bedeutet, dass Beobachter sich selbst und ihre Umwelt als Selektionen im Letzthorizont alles Sinns – also der Welt1 – auffassen müssen. «Welt in diesem Verständnis», so Luhmann in «Soziale Systeme», «ist das Korrelat der Identität von Sinn, sie ist in jedem Sinnelement ganz mitgegeben, und dies so, dass sie für alle Sinnelemente als dieselbe mitgegeben ist» (1984: 283). In «Gesellschaft der Gesellschaft» hält Luhmann diesbezüglich fest: «Sinn ist in allem, was aktualisiert wird, als Weltverweisung co-präsent» (1997: 49).
Unnegierbarkeit bedeutet, dass Welt wie Sinn eine differenzlose Kategorie ist. Wie der Sinn kann auch die Welt nicht negiert werden. Wie beim Sinn finden auch bei der Welt Operationen und Ausdifferenzierungen nur auf der markierten Innenseite der Zwei-Seiten-Form statt. Und doch: Wie die Form des Sinns den Unsinn so braucht die Zwei-Seiten-Form der Welt die «Leere, Nichtheit, das Chaos» (vgl. ebd.).
Welt als Welt1 ist die Summe und Einheit aller möglichen Sinnverweisungen.
^ ^ ^
Der Begriff der Welt2, Welt als Einheit der Differenz, beschreibt das Auftreten des Beobachters in Welt1. Indem sich Systeme durch ihre eigenen Operationen von Welt abkoppeln und operativ schliessen, totalisieren sie ihr Selbst im Verhältnis zu allem anderen. Dabei fungiert die Umwelt als «unmarked space» – als ein Leerkorrelat für die Erzeugung der Selbstreferenz des Systems.
˅ Welt als Einheit der Differenz
Die Diskussion über De-Ontologisierung zeigt, dass Luhmann nicht umhinkommt, für die Beschreibung der modernen Gesellschaft eine Minimalontologie zu verwenden, die aus Beobachter und Beobachtung besteht.
Mit der differenztheoretischen Perspektive auf den Weltbegriff W2 kommt nun der Beobachter ins Spiel. Luhmann führt ihn in «Soziale Systeme» mit der prominenten Setzung ein, dass es Systeme gibt (vgl. 1984: 39). Beobachter im systemtheoretischen Sinne sind sinnverarbeitende Systeme – also psychische und soziale Systeme.
Um den ontologischen Status des Beobachters besser zu verstehen, möchten wir an die zentrale Unterscheidung von Operation und Beobachtung erinnern. Wir diskutieren sie auch in den Abschnitten «Beobachten» und «Erkenntnis».
Operation bedeutet einerseits die Reproduktion der Elemente eines Systems durch die Elemente desselben Systems. Im Falle psychischer Systeme sind dies Gedanken und im Falle sozialer Systeme Kommunikationen. Wobei Beobachtungen die Voraussetzung für Gedanken und Kommunikationen sind. Damit es zu dieser autopoietischen Operationsweise kommen kann, müssen sich die Systeme zuerst von Welt abkoppeln und operativ schliessen.
Ein System kann eine Operation als Beobachten beobachten, indem es den operativen Vollzug des Beobachtens beobachtet. Dabei wird von einer Beobachtung erster Ordnung aus beobachtet, was beim Beobachten unterschieden und bezeichnet wird. Konkret bedeutet dies, dass Beobachter in Kommunikationen beobachten, was gesagt, geschrieben oder gedruckt wird. In dieser empirischen Beobachtung des Vollzugs des Beobachtens manifestiert sich die Realität eines Systems.
Durch Autopoiesis reproduzieren operativ geschlossene Systeme nicht nur sich selbst, sondern erzeugen zugleich eine Umwelt. «‹Die› Umwelt», so Luhmann in «Soziale Systeme», «ist nur ein Negativkorrelat des Systems. Sie ist keine operationsfähige Einheit, sie kann das System nicht wahrnehmen, nicht behandeln, nicht beeinflussen. Man kann deshalb auch sagen, dass durch Bezug auf und Unbestimmtlassen von Umwelt das System sich selbst totalisiert. Die Umwelt ist einfach ‹alles andere›» (1984: 249).
Mit anderen Worten: Im Vollzug des Beobachtens unterscheidet das System nur zwischen sich selbst und allem anderen. Es handelt sich dabei um eine asymmetrische Zwei-Seiten-Form, in der das System markiert ist und die Umwelt unmarkiert bleibt.
In «Die Gesellschaft der Gesellschaft» präzisiert Luhmann diesen Sachverhalt wie folgt: «In System/Umwelt-Beziehungen stehen Systeme, also jeweils die Innenseite der Form ‹System›, einem ‹unmarked space› (Spencer Brown) gegenüber, der vom System aus nicht erreicht und nicht – es sei denn inhaltsleer – bezeichnet werden kann. Die Referenz auf ‹die Umwelt› trägt nichts zu den Systemoperationen bei. ‹Die Umwelt› gibt keine Information. Sie ist nur ein Leerkorrelat für Selbstreferenz» (1997: 609).
Beobachtung andererseits bedeutet, dass ein System eine Operation als Beobachtung beobachtet, indem es die verwendete Unterscheidung beobachtet. Dabei wird von einer Beobachtung zweiter Ordnung aus beobachtet, wie beim Beobachten unterschieden und bezeichnet wird.
Bei dieser Beobachtungsweise spielt die basale Unterscheidung von Selbstreferenz und Fremdreferenz eine zentrale Rolle. Sie ist notwendig, damit ein System neben dem operativen auch einen kognitiven Unterschied zwischen sich selbst und der Umwelt machen kann. Aus diesem Grund hat Luhmann in der systemtheoretischen Erkenntnistheorie die vormoderne Unterscheidung von Sein und Nichtsein durch die Unterscheidung von Selbstreferenz und Fremdreferenz ersetzt (vgl. 1997: 911).
Die Bedingung der Möglichkeit der Unterscheidung von Selbstreferenz und Fremdreferenz ist die Wiedereinführung der Unterscheidung von System und Umwelt auf der Seite des Systems. Sie ermöglicht die Reflexion der Systemreferenzen. Das heisst, die Fähigkeit, sich auf sich selbst oder auf etwas anderes zu beziehen. «Die Differenz System/Umwelt», so Luhmann, «kommt zweimal vor: als durch das System produzierter Unterschied und als im System beobachteter Unterschied» (1997: 45).
Im obigen Abschnitt haben wir den Weltbegriff als Einheit der Möglichkeiten (Welt1) und in diesem Abschnitt als Einheit der Differenz (Welt2) diskutiert. Mit Luhmann können wir diese beiden Perspektiven wie folgt zusammenfassen: «Ursprünglich und phänomenologisch erfasst ist die Welt als unfassbare Einheit gegeben [Welt1, Anm. CMS]. Durch Systembildung und relativ auf Systembildung wird sie bestimmbar als Einheit einer Differenz [Welt2, Anm. CMS]. In beiden Hinsichten gilt: der Weltbegriff bezeichnet eine Einheit, die nur für Sinnsysteme aktuell wird, die sich von ihrer Umwelt zu unterscheiden vermögen und daraufhin die Einheit dieser Differenz reflektieren als Einheit, die zwei Unendlichkeiten, die innere und äussere, umfasst» (1984: 283f.).
Welt als Welt2 ist für ein System die Totalisierung des Selbst relativ zu allem anderen.
^ ^ ^
Der Begriff der Welt3, Welt als Einheit des Codes, nimmt die System-zu-System-Beziehungen in den Blick. Im Unterschied zur Welt2 fungiert jetzt die Umwelt nicht mehr als «unmarked space», sondern spezifische Umwelt mit anderen Systemen. Für die Beobachtung solcher Weltausschnitte bedarf es spezifischer Codes und Programme, die jeweils die Identität der verschiedenen Systeme definieren und Kommunikationen entsprechend zuordnen.
˅ Welt als Einheit des Codes
Bevor wir auf die medientheoretische Perspektive des Luhmannschen Weltbegriffs W3 eingehen, müssen wir bei der oben diskutierten differenztheoretischen Perspektive bleiben und den Begriff der Systemdifferenzierung kurz beleuchten.
Dem Mechanismus der Ausdifferenzierung widmet Luhmann in «Die Gesellschaft der Gesellschaft» ein ganzes Kapitel (vgl. 1997: 595 ff.). Ausgangspunkt seiner Beobachtungen ist die Unterscheidung von Gesellschaftssystem und Systemdifferenzierung.
Das Gesellschaftssystem differenziert sich nach Luhmann in der Welt1 aus: «Eine solche Ausdifferenzierung kann […] im nicht bezeichneten (erst durch die Ausdifferenzierung dann bezeichenbaren) Bereich sinnhafter Möglichkeiten erfolgen, also in der nicht weiter eingeschränkten Welt» (1997: 597).
Von Systemdifferenzierung spricht Luhmann, wenn sich innerhalb des Gesellschaftssystems weitere Teilsysteme ausdifferenzieren. Wichtig dabei ist, dass sich die Teilsysteme nicht nach dem Beobachtungsschema Ganzes/Teile, sondern nach dem Schema System/Umwelt konstituieren: «Vielmehr rekonstruiert jedes Teilsystem das umfassende System, dem es angehört und das es mitvollzieht, durch eine eigene (teilsystemspezifische) Differenz von System und Umwelt» (ebd.: 598).
Die Umstellung des Beobachtungsschemas von Ganzes/Teile auf System/Umwelt eröffnet neue Perspektiven für die Gesellschaftsanalyse. So kann Gesellschaft entweder hinsichtlich der System-Umwelt-Beziehung oder der System-zu-System-Beziehung beobachtet werden.
Für die Beobachtung der System-Umwelt-Beziehung ist die differenztheoretische Perspektive relevant. Sie beschreibt diese Beziehung anhand einer asymmetrischen Zwei-Seiten-Form, in der die unmarkierte Seite als Leerstelle für die Selbstreferenz des Systems fungiert.
«Nur mit der Unterscheidung von System und Umwelt», so Luhmann, «erfasst das System die Welteinheit bzw. die Einheit des umfassenden Systems, und zwar mit einer jeweils selbstbezüglichen Unterscheidung» (ebd. 600). Wir haben es bei dieser Perspektive also mit dem Weltbegriff W2 zu tun. Er gründet in einer universalistischen Operationsweise des Systems: «das heisst in der Form eines Schnitts durch die Welt» (ebd.: 609).
Für die Beobachtung der System-zu-System-Beziehung hingegen ist die medientheoretische Perspektive relevant. Anhand der Zwei-Seiten-Form lässt sich diese Beziehung nun als Einheit der Differenz von System und Umwelt beschreiben. Dies bedeutet, dass die Umwelt an den Operationen des Systems mitwirkt.
«Mit System-zu-System-Beziehungen […]», erklärt Luhmann weiter, «erfasst es [das System, Anm. CMS] nur Welt- bzw. Gesellschaftsausschnitte. Gerade diese Ausschnitthaftigkeit ermöglicht es dann aber, das jeweils andere System als System-in-einer-eigenen-Umwelt zu beobachten und damit die Welt bzw. die Gesellschaft aus der Perspektive des Beobachtens von Beobachtungen (Beobachtungen zweiter Ordnung) zu rekonstruieren» (ebd. 600). Bei dieser Perspektive haben wir es also mit dem Weltbegriff W3 zu tun. Er gründet in einer spezifischen Operationsweise des Systems: «das heisst in bestimmten kontingenten Beobachtungsweisen» (ebd.: 609).
Anhand der Unterscheidung von universalistischer und spezifischer Operationsweise haben wir die medientheoretische Perspektive auf den Weltbegriff W3 unter der Hand eingeführt. Zunächst ist zu klären, von welchem Medienbegriff bzw. Medientyp hier ausgegangen wird.
Entsprechend den drei Unwahrscheinlichkeitsarten von Kommunikation (Verstehen, Erreichen, Erfolg) unterscheidet Luhmann drei Medientypen. Die sogenannten symbolisch generalisierten Kommunikationsmedien transformieren die Unwahrscheinlichkeit des Erfolgs einer Kommunikation in Wahrscheinlichkeit. Sie haben die Funktion, in Fällen, in denen eine Ablehnung wahrscheinlich ist, die Annahme einer Kommunikation erwartbar zu machen. Deshalb werden sie auch Erfolgsmedien genannt.
Damit Erfolgsmedien funktionieren, benötigen sie einen Code (ebd.: 359 ff.). Ein Code besteht aus zwei Werten und schliesst weitere Werte aus. Der Code, der beispielsweise den Medienbereich des Wissenschaftssystems abdeckt, lautet: «wahr/falsch». Wissenschaftskommunikation orientiert sich immer an dieser Leitunterscheidung. An diesem Beispiel wird die grundlegende Funktion des Codes deutlich.
Der Code überführt die Annahme oder Ablehnung eines Sinnangebots, einer mitgeteilten Information, in ein Entweder/Oder. Es gibt kein Vielleicht. Watzlawick et al. unterscheiden im Zusammenhang mit «Menschlicher Kommunikation» diesbezüglich zwischen «analoger» und «digitaler» Kommunikation (vgl. 1969: 70 ff.).
Das Beispiel der Wissenschaftskommunikation zeigt zudem, dass es sich bei den Codes um sogenannte Präferenzcodes handelt. Das bedeutet, dass der positive Wert («wahr») gegenüber dem negativen Wert («falsch») bevorzugt wird. Mit der Präferenz des positiven Werts wird die Kommunikation gegen die Wahrscheinlichkeit des negativen Werts gesteuert.
Erfolgsmedien und ihre Codes sind quasi die Scharniere zwischen Weltbegriff W2 und W3.
Beobachtet ein System andere Systeme in seiner Umwelt, dann entscheidet es anhand des Codes, ob ein Sinnangebot in seinen Medienbereich gehört oder nicht. In dieser Hinsicht operiert das System universalistisch. Es unterscheidet zwischen sich selbst und allem anderen («unmarked state)». Falls ein Sinnangebot in den eigenen Bereich gehört, ist das entsprechende Erfolgsmedium allein zuständig. Das System operiert nun spezifisch. Es beobachtet den für seine Operationen relevanten Weltausschnitt.
«Der Universalismus», so Luhmann, «betrifft den weltweiten, durch externe Umstände nicht eingeschränkten Anwendungsbereich, die Spezifizität betrifft die Unterscheidung (hier: den Code), die dem Beobachten zugrunde liegt» (1997: 375 f.).
Wenn ein Sinnangebot dem eigenen Medienbereich zugeordnet wird, dann muss das System beide Seiten der Form des Codes nutzen können. Da auch der Code eine Zwei-Seiten-Form bildet, ist dies durch Kreuzen der Grenze möglich. In unserem Beispiel bedeutet dies, dass die Wissenschaftskommunikation sowohl mit dem positiven Wert «wahr» als auch mit dem negativen Wert «falsch» operieren kann.
Da der Code ein Sinnangebot einem Medienbereich nur zuordnet, bedarf es eines weiteren Mechanismus, der bestimmt, ob das Angebot dem positiven oder negativen Wert des Codes zuzurechnen ist. Diese Funktion übernehmen die sogenannten Programme. In der Wissenschaft wären dies beispielsweise Theorien und Methoden.
Der Code und die Programme haben die Aufgabe, die Einheit eines Systems in Abgrenzung zu anderen Systemen in seiner Umwelt zu spezifizieren.
Welt als Welt3 ist für ein System immer ein Weltausschnitt, der ein System anhand der Einheit seines Codes konstruiert.
^ ^ ^
Erkenntniskategorien
Die analytische Auflösung des Luhmannschen Weltbegriffs erlaubt es uns, Parallelen zur Kategorienlehre von Charles Sanders Peirce zu ziehen.
In der Philosophiegeschichte sind die Kategorienlehren von Aristoteles und Kant die wichtigsten Wegweiser für einen realistischen bzw. idealistischen Versuch, die Inhalte menschlicher Erfahrung zu organisieren. Grob gesagt bezieht sich die Lehre des Aristoteles auf das Seiende und diejenige Kants auf die Grundbegriffe des Denkens. Da Peirce sich weder als Realist noch als Idealist verstand, erkundete er mit seinem pragmatischen Ansatz eine dritte Position.
In seiner Kategorienlehre behandelt Peirce die Natur der Erfahrung selbst, die sowohl das Seiende als auch die Grundbegriffe des Denkens umfasst. Wie Luhmann ist er nicht an der vormodernen Unterscheidung von Subjekt und Objekt interessiert. Vielmehr lässt er sich von der Unterscheidung zwischen Erkennen und Erkanntem leiten.
Peirce reduziert die zehn Kategorien des Aristoteles bzw. die zwölf Kategorien Kants auf drei Kategorien, nämlich Erstheit, Zweitheit und Drittheit (vgl. Scheibmayr 2004: 17 ff.) Sie bilden die logische, phänomenologische und ontologische Grundstruktur der Erkenntnis.
Erstheit, Zweitheit und Drittheit sind irreduzibel und vollständig. Weder kann eine der Kategorien auf eine der beiden anderen zurückgeführt werden, noch ist eine Erkenntnis möglich, die nicht als eine Kombination der drei analysiert werden könnte.
Darüber hinaus impliziert jede höhere Kategorie die jeweils niedrigere Kategorie. Zweitheit impliziert Erstheit. Drittheit impliziert Zweitheit und Erstheit. Die Kategorien sind in jeder Erkenntnis gegeben. Das heisst, sie treten immer gemeinsam auf und werden nur zu analytischen Zwecken voneinander getrennt.
Schliesslich können die Kategorien auch als Relationen aufgefasst werden. Erstheit bildet eine nomadische, Zweitheit eine dyadische und Drittheit eine triadische Relation.
Die reine Präsenz der Kategorie der Erstheit entspricht in der Erkenntnis der Seinsweise der Möglichkeit. Erstheit ist eine monadische Relation.
˅ Erstheit
Die Erstheit ist schwer mit Begriffen zu fassen, weil sie ihnen vorausgeht. In «A Guess at the Riddle» schreibt Peirce: «It precedes all synthesis and all differentiation: it has no unity and no parts. It cannot be articulately thought: assert it, and it has already lost its characteristic innocence; for assertion always implies a denial of something else» (EP 1.248).
Brian Kemple nennt in seinem Buch «The Intersection of Semiotics and Phenomenology» drei Eigenschaften der Erstheit: Gegenwärtigkeit, Qualität des Gefühls und Selbstsein. Seine phänomenologische Analyse dieser Eigenschaften expliziert er an zwei Textstellen von Peirce (vgl. 2019: 137 ff.).
Anhand des Textes «On a New List of Categories», genauer anhand des dritten Paragraphen des Textes, interpretiert Kemple die Eigenschaften der Gegenwärtigkeit und des Selbstseins. Der dritte Paragraph beginnt mit der Aussage: «That universal conception which is nearest to sense is that of the present, in general. This is a conception, because it is universal» (EP 1.1).
Peirce unterscheidet in dieser Aussage zwischen Sinnesempfindung («sense») und Gegenwärtigkeit («present»). Letztere wird als Vorstellung («conception») aufgefasst, weil sie universell ist. Das heisst, der Geltungsanspruch dieser Vorstellung umfasst alle Erkenntnis.
Damit wir zu universellen Vorstellungen gelangen, müssen wir von konkreten Erfahrungen, die den Sinnesempfindungen eigen sind, abstrahieren. Dabei korrespondiert der Grad der Universalität der Vorstellung direkt dem Grad Abstraktion von den Sinnesempfindungen. Also ist die universelle Vorstellung, die den Sinnesempfindungen am nächsten ist, diejenige, die am wenigsten von ihr abstrahiert. Folglich muss die Gegenwärtigkeit am nächsten bei den Sinnesempfindungen sein.
Kemple interpretiert diesen Sachverhalt so, dass der Inhalt der Gegenwärtigkeit sich nicht klar vom Inhalt der Sinnesempfindungen unterscheiden lässt. «[…] there is no grasp of the distinction between formal object and material object; rather, something must be different in the manner of experiencing itself» (2019: 139).
Mit der eingangs zitierten Aussage grenzt sich Peirce von der idealistischen und der realistischen Position ab und postuliert eine dritte Position, indem er Erfahrung als Einheit der Differenz von Erfahren und Erfahrenem auffasst.
Der Unterschied, der diesen Unterschied ausmacht, liegt in der Aufmerksamkeit. Denn die Aufmerksamkeit und nicht die Sinnesempfindungen macht Objekte dem Denken gegenwärtig. Es muss also einen Unterschied zwischen der Gegenwärtigkeit der Aufmerksamkeit und der Gegenwärtigkeit der Sinnesempfindungen geben.
Die Gegenwärtigkeit der Aufmerksamkeit beschreibt Peirce im dritten Paragraphen als «[…] the conception of what is present in general, which is nothing but the general recognition of what is contained in attention» (EP 1.1). Sie ist nichts Anderes als die allgemeine Anerkennung dessen, was in der Aufmerksamkeit enthalten ist. Die Gegenwärtigkeit der Sinnesempfindungen indes führt zu einer konkreten Vorstellung dessen, worauf die Aufmerksamkeit gerichtet ist.
Im Erfahren der Gegenwärtigkeit im Allgemeinen als das, worauf die Aufmerksamkeit des Denkens gerichtet ist, liegt die Erfahrung der Gegenwart selbst. Peirce spricht in diesem Zusammenhang vom ES («it»), das jedem Unterscheiden und Vergleichen vorausgeht: «Before any comparison or discrimination can be made between what is present, what is present must have been recognized as such, as it […]» (EP 1.1).
Kemple fasst seine Interpretation des dritten Paragraphen von «On a New List of Categories» mit folgenden Worten zusammen: «The category of Firstness, as an element present in every species-specifically human cognitive activity, is the experience of the pure presence belonging to the experiencing of an object as something not contained in the sense data but co-present with it. More generally, however, the pure presence of the category of Firstness is the mode of being of possibility» (2019: 140). Erstheit ist demnach die Seinsweise der Möglichkeit. Diese Aussage expliziert er an einem zweiten Textabschnitt von Peirce.
In «Sundry Logical Conceptions» schreibt Peirce: «Possibility, the mode of being of Firstness, is the embryo of being. It is not nothing. It is not existence. We not only have an immediate acquaintance with Firstness in the qualities of feelings and sensations, but we attribute it to outward things. […] In fact, it seems undeniable that there really are such possibilities, and that, though they are not existences, they are not nothing. They are possibilities, and nothing more. But whether this be admitted or not, it is undeniable that such elements are in the objects as we commonly conceive them; and that is all that concerns phenomenology» (EP 2.268-269).
Wir erleben Möglichkeit durch die unmittelbare Gegenwärtigkeit von Objekten und durch die ihnen entsprechende Qualität von Gefühlen und Empfindungen. Diese Qualität der Gefühle und Empfindungen macht uns mit den Möglichkeiten der Objekte vertraut, weil sie deren Potenziale aufzeigen. Erstheit ist unvermittelt, weil sie direkt erlebt wird und nicht durch Analyse oder Synthese entsteht.
Andererseits schreiben wir gefühlten und empfundenen Qualitäten auch den Objekten zu. Erstheit ist also nicht nur ein inneres Erleben, sondern auch eine Eigenschaft der Objekte in der Welt.
Die Gegenwärtigkeit der Möglichkeiten geht nicht allein von den Subjekten aus, sondern auch von den Objekten. Das bedeutet, dass Möglichkeit nicht nur eine subjektive Vorstellung ist, sondern auch eine objektive Eigenschaft von Objekten. Die Möglichkeiten sind weder Existenzen noch sind sie Nichts. Sie sind etwas Drittes. Sie sind nach Kemple unverwirklichte vage Sein-Können («the unrealized vague could-be»).
Die «Sundry Logical Conceptions» einleitend definiert Peirce Erstheit wie folgt: «Firstness is that which is such as it is positively and regardless of anything else» (EP 2.267). Erstheit ist Selbstein. Sie ist eine monadische Relation. Daraus leitet Scheibmayer in seiner Studie «Niklas Luhmanns Systemtheorie und Charles S. Peirces Zeichentheorie» weitere Eigenschaften der Erstheit ab (2004: 186 ff.).
Phänomene der Erstheit wie die Qualität der Gefühle müssen eindeutig sein, weil sie positiv und unabhängig von allem anderen sind. Da es in dieser Kategorie noch keine Beobachter und damit auch keine Beobachtungen gibt, hat die Eindeutigkeit des Selbstseins keinen Informationswert. Mit anderen Worten können wir sagen: Die Eindeutigkeit des Selbstseins wird postuliert, weil sie nicht beobachtet werden kann.
Die monadische Relation der Erstheit steht für die Gegenwärtigkeit der Möglichkeiten positiver Eigenschaften und Qualitäten. Sie steht nicht für eine Identität. Dazu bräuchte es die dyadische Relation der Zweitheit. Und sie steht nicht für ein Gesetz. Denn dazu bräuchte es zusätzlich die triadische Relation der Drittheit.
^ ^ ^
Die Kategorie der Zweitheit entspricht in der Erkenntnis der Seinsweise der Aktualisierung einer Möglichkeit. Dies geschieht durch eine raum-zeitlich fixierte Aktualisierung der Identität von etwas im Gegensatz zu etwas anderem. Deshalb ist Zweitheit eine dyadische Relation.
˅ Zweitheit
Im Unterschied zur Erstheit ist Zweitheit die fassbarste Kategorie. Peirce schreibt in den «Sundry Logical Conceptions» über Zweitheit: «We talk of hard facts. That hardness, that compulsiveness of experience, is Secondness. A door is slightly ajar. You try to open it. Something prevents. You put your shoulder against it, and experience a sense of effort and a sense of resistance. These are not two forms of consciousness; they are two aspects of one two-sided consciousness» (EP 2.268).
Zweitheit ist die Kategorie der Aktion und Reaktion. Mit ihnen geht das Erleben der Sinnesempfindung der Anstrengung («sens of effort») und des Widerstands («sens of resistance») einher. Es handelt sich dabei nicht um zwei voneinander getrennte Bewusstseinszustände, sondern vielmehr um zwei untrennbare Seiten eines Bewusstseinszustands.
Kemple betont in seiner Interpretation dieses Zitats die Einheit solcher zweiseitigen Bewusstseinszustände: «Secondness as an element of conscious experience is undivided; but simultaneously, provisions the possibility of realizing a Second» (2019: 142). Er argumentiert, dass wir eine beabsichtigte Handlung («sens of effort») und einen Widerstand («sens of resistance») eben nicht als voneinander getrennte Seinsweisen erleben. Vielmehr erleben wir den Widerstand gegen das Beabsichtigte als eine Art von Einheit.
Mit anderen Worten: Zweitheit ist die Einheit der Differenz von Reaktion und Aktion. Nach Kemple ermöglicht Zweiheit das Erleben der Verbundenheit zu etwas Anderem. Diese Verbundenheit besteht nicht bloss in der Gegenwärtigkeit des Anderen (Erstheit), sondern in dessen Gegenwärtigkeit im Gegensatz zu sich selbst. «Secondness», so Kemple, «is the experience of worldly interruption in the otherwise smooth continuum of subjectivity» (ebd.).
In seinen «Logical Tracts. No. 2» beschreibt Peirce die Zweitheit wie folgt: «To say that a thing exists is to say that it reacts with the other things in the universe, being other than every one of them. Hence existence is a conception of which Secondness is the principal ingredient. Secondness may be abstractly defined as a mode of being which consists in something, A, and something, B, being each as it is, A in B’s being as it is, and B in A’s being as it is, entirely regardless of any third» (2021: 2109).
Nach Scheibmayer macht dieser Textauszug deutlich, dass Zweitheit die Kategorie der dyadischen Relation ist (vgl. 2004: 173 ff.). Diese Relation kommt beispielsweise in zwei Dingen zum Ausdruck, die sich gegenseitig dazu bestimmen, so zu sein, wie sie sind. Peirce subsumiert unter der Kategorie der Zweitheit nicht nur Dinge, sondern den ganzen Bereich der Existenz, der Wirklichkeit, der Tatsachen, des Erlebens von Aktion und Reaktion. Scheibmayer betont in diesem Zusammenhang, dass Dinge oder Ereignisse ihre Identität und Individualität nicht per se haben, sondern der Differenz der Zweitheit verdanken.
Die Kategorie der Zweitheit entspricht der Aktualisierung einer Möglichkeit (Erstheit). Dies kann immer nur im Hier und Jetzt geschehen. Deshalb ist Zweitheit nicht generalisierbar. Sie ist weder wiederholbar noch revidierbar. Aus diesem Grund kommen nach Scheibmayer die Phänomene der Zweitheit den Einzeldingen und Ereignissen am nächsten: «Die Aktualität von Ereignissen ist auf einen Zeitpunkt reduziert, so dass die für die Zweitheit geforderte räumlich-zeitliche Fixierung hier am deutlichsten ausgeprägt ist» (ebd.: 174).
^ ^ ^
Erkenntnis
Niklas Luhmann kann zweifellos als Konstruktivist bezeichnet werden. Seine Erkenntnistheorie lässt sich jedoch nur schwer in die Unterscheidung von schwachem und radikalem Konstruktivismus einordnen. Am treffendsten ist für sie wohl die Bezeichnung «operativer Konstruktivismus».
Luhmann stimmt mit dem radikalen Konstruktivismus dahingehend überein, dass er in der Formulierung der erkenntnistheoretischen Problemstellung von «obwohl» auf «weil» umstellt. In «Erkenntnis als Konstruktion» hält er fest, dass sich der schwache Konstruktivismus fragt, wie Erkenntnis möglich ist, obwohl sie keinen Zugang zur Realität hat. Die radikale Antwort darauf lautet, dass Erkenntnis möglich ist, weil sie keinen Zugang zur Realität hat (vgl. 1988: 9 f.).
Diese radikalkonstruktivistische Antwort erweitert Luhmann um die weiterführende Frage, wie die Abkopplung von der Welt als Bedingung der Möglichkeit der Erkenntnis von Welt überhaupt möglich ist. Zur Beantwortung dieser Frage gibt er die Unterscheidung von Subjekt und Objekt auf und führt stattdessen die Unterscheidung von System und Umwelt ein. Im Kontext dieser Unterscheidung wird Erkenntnis als Operation eines erkennenden Systems – nicht Subjekts – verstanden, das nicht unmittelbar auf eine externe Realität zugreifen kann, sondern durch interne Prozesse eine eigene Wirklichkeit konstruiert.
^ ^ ^
˅ System und Umwelt
Luhmann gibt in seiner Erkenntnistheorie die Unterscheidung von Subjekt und Objekt auf und führt stattdessen die Unterscheidung von System und Umwelt ein. Damit umgeht er ein Problem der klassischen Erkenntnistheorie, der zufolge Erkenntnis und Erkenntnisgegenstand über unterschiedliche Seinsweisen verfügen. Descartes hatte diese Seinsweisen anhand der Unterscheidung von «res cogitans» (denkende Substanz) und «res extensa» (ausgedehnte Substanz) formuliert. Sie führen nach Luhmann sowohl in subjektzentrierten als auch in objektzentrierten Theorien in eine erkenntnistheoretische Sackgasse.
In Luhmanns Erkenntnistheorie gibt es keine unterschiedlichen Seinsweisen von System und Umwelt. In «Erkenntnis als Konstruktion» schreibt er: «Wir gehen davon aus, dass alle erkennenden Systeme reale Systeme in einer realen Umwelt sind, mit anderen Worten: dass es sie gibt» (1988: 14). Mit diesem Satz bezieht er sich auf die viel zitierte Aussage in «Soziale Systeme», gemäss der er davon ausgeht, dass es soziale Systeme gibt (vgl. 1984: 30). Diese Position impliziert, dass die systemtheoretische Erkenntnistheorie auf realen Bedingungen beruht, auch wenn sie an der konstruktivistischen Tradition anschliesst.
Wenn wir mit Luhmann von unterschiedlichen Seinsweisen absehen und einen konstitutiven Zusammenhang zwischen System und Umwelt annehmen, dann stellt sich jedoch die Frage, wie denn Differenzierung im Sinne der Abkopplung von Welt möglich ist. Oder mit anderen Worten: Wie kommt es dazu, dass Systeme sich operativ schliessen und gegenüber ihrer Umwelt dennoch offen bleiben?
Die Abkopplung eines Systems von Welt bzw. dessen Schliessung ist nach Luhmann nur möglich, indem es eigene Operationen produziert und im Netzwerk ihrer rekursiven Vor- und Rückgriffe reproduziert (vgl. 1988: 15). Durch diese autopoietische Operationsweise erzeugt es die Differenz von System und Umwelt und hält sie aufrecht. Dadurch schafft das System auch seine spezifische Umwelt, die von seiner Struktur und seinen Operationen geformt wird.
Da das operativ geschlossene System nicht in seiner Umwelt operieren kann, führt es die Differenz von System und Umwelt auf der Seite des Systems wieder ein. Durch die Wiedereinführung wird die Unterscheidung von System und Umwelt im System so reproduziert, dass es sich selbst oder seine Umwelt bezeichnen und reflektieren kann. Diese Art der Selbstbeobachtung und Selbstbeschreibung ermöglicht es dem System, seine eigene Identität und seine eigenen Operationen im Kontext seiner Umwelt zu verstehen und anzupassen.
^ ^ ^
Die Umstellung der erkenntnistheoretischen Unterscheidung von Subjekt und Objekt auf System und Umwelt ermöglicht nicht nur, die Abkopplung und Schliessung von Systemen zu erklären. Sie liefert auch den Ausgangspunkt für eine Theorie beobachtender Systeme.
˅ Beobachtung als Paradoxie
«Erkenntnis», hält Luhmann in «Erkenntnis und Konstruktion» fest, «wird […] durch die Operationen des Beobachtens und des Aufzeichnens von Beobachtungen (Beschreibungen) angefertigt» (2023: 16). Beobachtungen und Beschreibungen können sich auf den Beobachter selbst oder auf andere Systeme in seiner Umwelt beziehen. Zudem können sich Beobachtungen erster Ordnung auf den Vollzug eigener oder fremder Beobachtungen und Beobachtungen zweiter Ordnung auf Erkenntnisse über das eigene oder fremde Beobachtungen beziehen.
Beobachtungen erster oder zweiter Ordnung sind immer Eigenleistungen eines Beobachters. Das bedeutet, dass die Art und Weise, wie ein Beobachter Systeme in seiner Umwelt beobachtet, von seinen strukturellen Eigenschaften und internen Unterscheidungen abhängt. Die Umwelt selbst enthält keine vorgefertigten Unterscheidungen, die vom Beobachter direkt übernommen werden könnten.
Im Anschluss an Spencer-Brown fasst Luhmann Beobachten als Unterscheiden und Bezeichnen auf. Der Begriff des Beobachtens wurde oben bereits ausführlich behandelt. Im Folgenden werden wir auf spezifische Aspekte im Kontext der Erkenntnistheorie hinweisen. Dabei spielen insbesondere die Begriffe «Operation» und «Paradoxie» zentrale eine Rolle.
Wie anhand der Unterscheidung von Operation und Beobachtung diskutiert, ist die Unterscheidung, die ein Beobachter verwendet, für ihn selbst immer blind. Der Beobachter kann nicht gleichzeitig die Operation des Beobachtens ausführen und die dabei verwendete Unterscheidung beobachten. Eine solche Beobachtung müsste zugleich etwas und sich selbst unterscheiden.
Die eigene Beobachtung ist also für die Beobachtung des Beobachters ein blinder Fleck. So wie der blinde Fleck im eigenen Auge eine Voraussetzung für das Sehen ist, so ist der blinde Fleck der eigenen Beobachtung konstitutiv für das Beobachten.
Die rein analytische Unterscheidung von Operation und Beobachtung ist für Luhmann deshalb wichtig, weil er damit das Phänomen der Paradoxie besser fassen kann: «Als Operation kann das Beobachten vollzogen und als empirischer Vollzug beobachtet werden. Als Beobachtung ist es paradox» (vgl. 1990: 95). Weil die eigene Blindheit die Bedingung der Möglichkeit des Beobachtens ist, ist Beobachten in seinem empirischen Vollzug eine paradoxe Operation.
Erst die Unterscheidung von Operation und Beobachtung erlaubt es, die Paradoxie des Beobachtens zu entfalten: Zwar kann die Beobachtung sich selbst nicht beobachten, aber sie kann beobachtet werden. Die Möglichkeit, Beobachtungen zu beobachten, ist durch die Beobachtung zweiter Ordnung gegeben.
^ ^ ^
Die systemtheoretische Erkenntnistheorie hat den Widerspruch aufzulösen, wie Erkenntnis von Welt durch Abkopplung von Welt möglich ist. Mit der Unterscheidung von System und Umwelt haben wir gesehen, dass sich Systeme durch operative Schliessung von ihrer Umwelt abschliessen. Und mit der im letzten Unterabschnitt diskutierten Unterscheidung von Operation und Beobachtung haben wir erfahren, dass wir eine Beobachtung als eine Paradoxie auffassen können.
Die Paradoxie der Beobachtung, also die Tatsache, dass sie nicht gleichzeitig etwas und sich selbst unterscheiden kann, zwingt das System zur Beobachtung von Beobachtungen und konstituiert so einen kontinuierlichen Prozess von Beobachtungen zweiter Ordnung.
Die Auflösung des Widerspruchs von operativer Geschlossenheit und kognitiver Offenheit liegt also in der Paradoxie der Beobachtung selbst. Sie macht es möglich, dass die Resultate des operativen Vollzugs von Beobachtungen zum Gegenstand neuer Operationen des Beobachtens werden.
Mit der prominenten Stellung, die die Paradoxie in der systemtheoretischen Erkenntnistheorie einnimmt, verabschiedet sich Luhmann von der klassischen Logik. Nach ihr sind beim Beobachten und Beschreiben von Welt sogenannte Zirkelschlüsse («petitio principii») zu vermeiden, weil sie zu paradoxen Aussagen führen. Luhmann postuliert stattdessen die Zulässigkeit einer Methodik, die Selbstreferenz zulässt und damit die Paradoxie zum Ausgangspunkt von Erkenntnis macht.
Gleichzeitig stellt er die axiomatisch-deduktive Theorie in Frage und setzt an ihre Stelle eine ausgeklügelte Theorie des Beobachtens, die im Anschluss an Gorge Spencer-Brown auf einem formalen Begriff des Beobachtens abgestellt ist.
Obwohl der Systemtheorie nachgesagt wird, sie sei viel zu abstrakt, um als empirische Theorie nutzbar zu sein, weist Luhmann immer wieder auf ihre Realitätsbezüge hin. Denn Beobachten ist eine empirische, also beobachtbare Operation.
Die soziale Welt, wie sie für sinnprozessierende Systeme vorkommt, ist demnach eine beobachtete Welt. Und die Bedingungen der Möglichkeit der unterschiedlichen Hinsichten auf diese Welt liegen im Beobachten selbst. Die Theorie des Beobachtens beruht auf Immanenz. Damit grenzt sich Luhmann auch von jeglichen transzendentalen Erkenntnistheorien ab.
Schliesslich unterstellt Luhmann seiner Theorie des Beobachtens keine Ontologie, sondern ihn interessiert vielmehr die Ontogenese einer Ontologie bzw. einer sogenannt fungierenden Ontologie (vgl. Fuchs 2015: 11). Es geht ihm also nicht darum, zu zeigen, was ein Beobachter in der sozialen Welt als soziale Tatsache erkennen kann, sondern vielmehr darum, zu erklären, wie es kommt, dass einem Beobachter etwas als soziale Tatsache erscheint. Die Theorie des Beobachtens ist also eine Theorie der Ontogenese.